Contents
2つの集合の要素の個数の最大最小問題2

ヒロ
次も実際に定期テストで出題された問題。
問題海外旅行者100人のうち,75人が風邪薬を,80人が胃薬を携帯していた。次のような人は,何人以上何人以下か。
(1) 風邪薬と胃薬を両方とも携帯した人
(2) 風邪薬と胃薬を両方とも携帯していない人
(1) 風邪薬と胃薬を両方とも携帯した人
(2) 風邪薬と胃薬を両方とも携帯していない人

ヒロ
自分で集合を設定して線分を利用して考えよう。
【考え方と解答】
海外旅行者100人を全体集合 $U$ とする。風邪薬を携帯している人の集合を $A$,胃薬を携帯している人の集合を $B$ とする。
(1) 風邪薬と胃薬を両方とも携帯した人を表す集合は $A\cap B$ である。つまり,線分を用いた図では重なり部分である。
最小値を考えると,重なり部分をできるだけ少なくなるように,線分を反対側から伸ばしていくため,次の図のようになる。
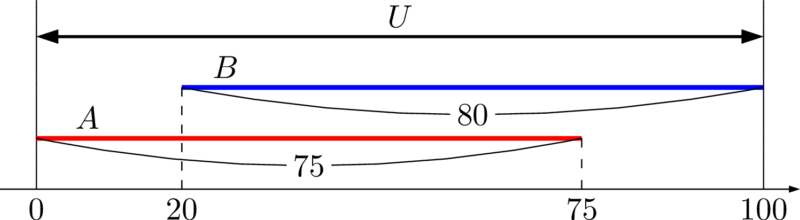
よって,$n(A\cap B)$ の最小値は
重なり部分をできるだけ多くなるように,両方の線分を左側から伸ばしていくため,次の図のようになる。
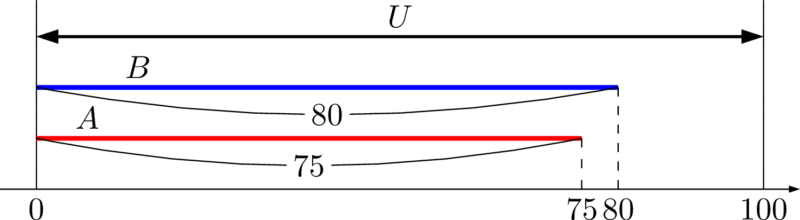
よって,$n(A\cap B)$ の最大値は
(2) 風邪薬と胃薬を両方とも携帯していない人を表す集合は $\overline{A}\cap\overline{B}$ である。
ド・モルガンの法則を利用すると,$n(\overline{A\cup B})$ となる。
つまり線分を用いた図では,線分がない部分である。
最小となるのは,$n(A\cup B)$ が最大になるときである。
これは $n(A\cap B)$ が最小になるときで,重なり部分をできるだけ少なくなるように,両方の線分を左側から伸ばしていくため,次の図のようになる。

よって,$n(A\cup B)$ の最大値が100であるから,$\overline{A}\cap\overline{B}$ の最小値は0である。
次に $\overline{A}\cap\overline{B}$ の最大値を考える。
逆に重なり部分をできるだけ多くなるように,両方の線分を左側から伸ばしていくため,次の図のようになる。

よって,$n(A\cup B)$ の最小値は80であるから,$\overline{A}\cap\overline{B}$ の最大値は20である。
したがって,風邪薬と胃薬を両方とも携帯していない人は0人以上20人以下である。
海外旅行者100人を全体集合 $U$ とする。風邪薬を携帯している人の集合を $A$,胃薬を携帯している人の集合を $B$ とする。
(1) 風邪薬と胃薬を両方とも携帯した人を表す集合は $A\cap B$ である。つまり,線分を用いた図では重なり部分である。
最小値を考えると,重なり部分をできるだけ少なくなるように,線分を反対側から伸ばしていくため,次の図のようになる。

よって,$n(A\cap B)$ の最小値は
\begin{align*}
75-20=55
\end{align*}
次に最大値を考える。75-20=55
\end{align*}
重なり部分をできるだけ多くなるように,両方の線分を左側から伸ばしていくため,次の図のようになる。

よって,$n(A\cap B)$ の最大値は
\begin{align*}
n(A)=75
\end{align*}
したがって,風邪薬と胃薬を両方とも携帯した人は55人以上75人以下である。n(A)=75
\end{align*}
(2) 風邪薬と胃薬を両方とも携帯していない人を表す集合は $\overline{A}\cap\overline{B}$ である。
ド・モルガンの法則を利用すると,$n(\overline{A\cup B})$ となる。
つまり線分を用いた図では,線分がない部分である。
最小となるのは,$n(A\cup B)$ が最大になるときである。
これは $n(A\cap B)$ が最小になるときで,重なり部分をできるだけ少なくなるように,両方の線分を左側から伸ばしていくため,次の図のようになる。

よって,$n(A\cup B)$ の最大値が100であるから,$\overline{A}\cap\overline{B}$ の最小値は0である。
次に $\overline{A}\cap\overline{B}$ の最大値を考える。
逆に重なり部分をできるだけ多くなるように,両方の線分を左側から伸ばしていくため,次の図のようになる。

よって,$n(A\cup B)$ の最小値は80であるから,$\overline{A}\cap\overline{B}$ の最大値は20である。
したがって,風邪薬と胃薬を両方とも携帯していない人は0人以上20人以下である。

ヒロ
複雑で良く分からないと嘆いていた人も,これで大丈夫だろう。



















