2020年センター試験 数学ⅡB 第4問 ベクトルの解説をします。
まだ問題を解いていない人は解いてから解説を読んでください。
\mathrm{A}(3,~3,~-6),~\mathrm{B}(2+2\sqrt{3},~2-2\sqrt{3},~-4)
\end{align*}
\Vec{OA}\perp\Vec{OC},~\Vec{OB}\Cdota\Vec{OC}=24~\cdots\cdots①
\end{align*}
(1) $\abs{\Vec{OA}}=\myBox{ア}\sqrt{\myBox{イ}}$, $\abs{\Vec{OB}}=\myBox{ウ}\sqrt{\myBox{エ}}$ であり,$\Vec{OA}\Cdot\Vec{OB}=\myBox{オカ}$ である。
(2) 点Cは平面 $\alpha$ 上にあるので,実数 $s,~t$ を用いて,$\Vec{OC}=s\Vec{OA}+t\Vec{OB}$ と表すことができる。このとき,①から $s=\dfrac{\myBox{キク}}{\myBox{ケ}}$,$t=\myBox{コ}$ である。したがって,$\abs{\Vec{OC}}=\myBox{サ}\sqrt{\myBox{シ}}$ である。
(3) $\Vec{CB}=\left(\myBox{ス},~\myBox{セ},~\myBox{ソタ}\right)$ である。したがって,平面 $\alpha$ 上の四角形OABCは $\myBox{チ}$。$\myBox{チ}$ に当てはまるものを,次の⓪~④のうちから一つ選べ。ただし,少なくとも一組の対辺が平行な四角形を台形という。
⓪ 正方形である
① 正方形ではないが,長方形である
② 長方形ではないが,平行四辺形である
③ 平行四辺形ではないが,台形である
④ 台形ではない
$\Vec{OA}\perp\Vec{OC}$ であるので,四角形OABCの面積は $\myBox{ツテ}$ である。
(4) $\Vec{OA}\perp\Vec{OD}$, $\Vec{OC}\Cdot\Vec{OD}=2\sqrt{6}$ かつ $z$ 座標が1であるような点Dの座標は
\left(\myBox{ト}+\dfrac{\sqrt{\myBox{ナ}}}{\myBox{ニ}},~
\myBox{ヌ}-\dfrac{\sqrt{\myBox{ネ}}}{\myBox{ノ}},~1\right)
\end{align*}
3点O,C,Dの定める平面を $\beta$ とする。また,$\alpha$ と $\beta$ は垂直であるので,三角形ABCを底面とする四面体DABCの高さは $\sqrt{\myBox{フ}}$ である。したがって,四面体DABCの体積は $\myBox{ヘ}\sqrt{\myBox{ホ}}$ である。
(1)の考え方と解答

まずはベクトルの大きさと内積という基本の確認。
$\Vec{OA}=(3,~3,~-6)$ より
\abs{\Vec{OA}}&=3\sqrt{1^2+1^2+(-2)^2} \\[4pt]
&=3\sqrt{6}
\end{align*}
\abs{\Vec{OB}}&=2\sqrt{(1+\sqrt{3})^2+(1-\sqrt{3})^2+(-2)^2} \\[4pt]
&=2\sqrt{12}=4\sqrt{3}
\end{align*}
\Vec{OA}\Cdota\Vec{OB}&=6\{(1+\sqrt{3})+(1-\sqrt{3})+4\} \\[4pt]
&=36
\end{align*}
(2)の考え方と解答
(2) 点Cは平面 $\alpha$ 上にあるので,実数 $s,~t$ を用いて,$\Vec{OC}=s\Vec{OA}+t\Vec{OB}$ と表すことができる。このとき,①から $s=\dfrac{\myBox{キク}}{\myBox{ケ}}$,$t=\myBox{コ}$ である。したがって,$\abs{\Vec{OC}}=\myBox{サ}\sqrt{\myBox{シ}}$ である。

2つのベクトルが垂直のときは内積が0になることを利用しよう。
$\Vec{OA}\perp\Vec{OC}$ より $\Vec{OA}\Cdot\Vec{OC}=0$ であるから
&\Vec{OA}\Cdota(s\Vec{OA}+t\Vec{OB})=0 \\[4pt]
&(3\sqrt{6})^2s+36t=0 \\[4pt]
&3s+2t=0
\end{align*}
&\Vec{OB}\Cdota(s\Vec{OA}+t\Vec{OB})=24 \\[4pt]
&36s+(4\sqrt{3})^2t=24 \\[4pt]
&3s+4t=2
\end{align*}

次は $\abs{\Vec{OC}}$ を求めよう。
$\Vec{OC}=-\dfrac{2}{3}\Vec{OA}+\Vec{OB}$ より
\abs{\Vec{OC}}^2&=\abs{-\dfrac{2}{3}\Vec{OA}+\Vec{OB}}^2 \\[4pt]
&=\dfrac{4}{9}\Cdota54-\dfrac{4}{3}\Cdota36+48 \\[4pt]
&=24-48+48 \\[4pt]
&=24
\end{align*}
(3)の考え方と解答
(3) $\Vec{CB}=\left(\myBox{ス},~\myBox{セ},~\myBox{ソタ}\right)$ である。したがって,平面 $\alpha$ 上の四角形OABCは $\myBox{チ}$。$\myBox{チ}$ に当てはまるものを,次の⓪~④のうちから一つ選べ。ただし,少なくとも一組の対辺が平行な四角形を台形という。
⓪ 正方形である
① 正方形ではないが,長方形である
② 長方形ではないが,平行四辺形である
③ 平行四辺形ではないが,台形である
④ 台形ではない
$\Vec{OA}\perp\Vec{OC}$ であるので,四角形OABCの面積は $\myBox{ツテ}$ である。

$\Vec{CB}$ の成分を求めよう。
$\Vec{OC}=-\dfrac{2}{3}\Vec{OA}+\Vec{OB}$ より
&\Vec{OB}-\Vec{OC}=\dfrac{2}{3}\Vec{OA} \\[4pt]&\Vec{CB}=\dfrac{2}{3}(3,~3,~-6) \\[4pt]&\Vec{CB}=(2,~2,~-4)
\end{align*}

次は四角形OABCの形状を決定する問題。
$\Vec{CB}=\dfrac{2}{3}\Vec{OA}$ より,CBとOAは平行である。
また $\mathrm{OC}\perp\mathrm{OA}$ であることを考えると,
四角形OABCは台形である。$\myBox{チ}=③$
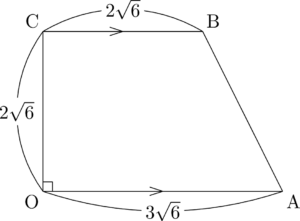

次は四角形OABCの面積を求めよう。
四角形OABCは上の図のような台形であるから,その面積は
\dfrac{1}{2}(2\sqrt{6}+3\sqrt{6})\Cdota2\sqrt{6}=30
\end{align*}
(4)の考え方と解答
(4) $\Vec{OA}\perp\Vec{OD}$, $\Vec{OC}\Cdot\Vec{OD}=2\sqrt{6}$ かつ $z$ 座標が1であるような点Dの座標は
\begin{align*}である。このとき $\kaku{COD}=\myBox{ハヒ}\Deg$ である。
\left(\myBox{ト}+\dfrac{\sqrt{\myBox{ナ}}}{\myBox{ニ}},~
\myBox{ヌ}-\dfrac{\sqrt{\myBox{ネ}}}{\myBox{ノ}},~1\right)
\end{align*}
3点O,C,Dの定める平面を $\beta$ とする。また,$\alpha$ と $\beta$ は垂直であるので,三角形ABCを底面とする四面体DABCの高さは $\sqrt{\myBox{フ}}$ である。したがって,四面体DABCの体積は $\myBox{ヘ}\sqrt{\myBox{ホ}}$ である。

与えられた条件から点Dの座標を求める問題。
$\Vec{OD}=(p,~q,~1)$ とおくと,$\Vec{OA}\perp\Vec{OD}$ より
&3p+3q-6=0 \\[4pt]&p+q=2~\cdots\cdots②
\end{align*}
\Vec{OC}&=-\dfrac{2}{3}\Vec{OA}+\Vec{OB} \\[4pt]&=-\dfrac{2}{3}(3,~3,~-6)+(2+2\sqrt{3},~2-2\sqrt{3},~-4) \\[4pt]&=(2\sqrt{3},~-2\sqrt{3},~0)
\end{align*}
&2\sqrt{3}p-2\sqrt{3}q=2\sqrt{6} \\[4pt]&p-q=\sqrt{2}~\cdots\cdots③
\end{align*}
よって,点Dの座標は
\left(1+\dfrac{\sqrt{2}}{2},~1-\dfrac{\sqrt{2}}{2},~1\right)
\end{align*}

次は $\kaku{COD}$ を求めよう。
点Dの座標より
\abs{\Vec{OD}}&=\sqrt{\left(1+\dfrac{\sqrt{2}}{2}\right)^2
+\left(1-\dfrac{\sqrt{2}}{2}\right)^2+1} \\[4pt]&=2
\end{align*}
$\Vec{OC}\Cdot\Vec{OD}=2\sqrt{6}$ より,$\mathrm{OH}=1$ と分かるから
$\sankaku{ODH}$ は $1:2:\sqrt{3}$ の直角三角形である。
$\mathrm{OH}:\mathrm{OD}=1:2$ より,$\kaku{COD}=60\Deg$

最後は四面体の体積を求める問題。
$\sankaku{ABC}$ の面積を $S$ とすると
S&=\dfrac{1}{2}\Cdota2\sqrt{6}\Cdota2\sqrt{6} \\[4pt]&=12
\end{align*}
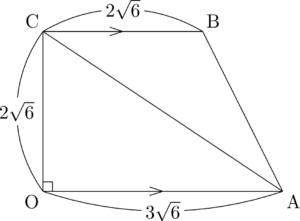
四面体DABCの高さは $\mathrm{DH}=\sqrt{3}$ であるから,求める体積は
\dfrac{1}{3}S\Cdota\mathrm{DH}&=\dfrac{1}{3}\Cdota12\Cdota\sqrt{3} \\[4pt]&=4\sqrt{3}
\end{align*}
2020年 センター数学ⅡB ベクトルを解いた感想

全体的に誘導通りに解いていくしかないため,それなりに時間がかかってしまうだろう。

何を求めなければならないのかを素早く判断して,それに瞬時に対応できるだけの実力を身に付けておくことが重要である。






















