Contents
複素数を利用した解法

ヒロ
複素数を利用した解法を説明しておくよ。

ヒロ
明らかに三角関数の問題に見える問題でも,視点を変えると,今後は極形式を利用した解法で解きたくなるかもしれない。

ヒロ
複素数の極形式を思い出そう。例えば,$x^n=1$ の解を考えよう。
【$x^n=1$ の解】
$x=r(\cos\theta+i\sin\theta)$ $(r>0,~0\leqq\theta<2\pi)$ とおくと,$\abs{x}=1$ より,$r=1$ である。このとき,
\begin{align*}
x^n&=(\cos\theta+i\sin\theta)^n \\[4pt]
&=(\cos n\theta+i\sin n\theta)
\end{align*}
となる。$x^n=1$ よりx^n&=(\cos\theta+i\sin\theta)^n \\[4pt]
&=(\cos n\theta+i\sin n\theta)
\end{align*}
\begin{align*}
&n\theta=2k\pi \\[4pt]
&\theta=\dfrac{2k\pi}{n}~(k=0,~1,~2,~\cdots,~n-1)
\end{align*}
よって,1の $n$ 乗根は $n$ 個あり,その $n$ 個が $\cos\dfrac{2k\pi}{n}+i\sin\dfrac{2k\pi}{n}$ $(k=0,~1,~2,~\cdots,~n-1)$ と表される。&n\theta=2k\pi \\[4pt]
&\theta=\dfrac{2k\pi}{n}~(k=0,~1,~2,~\cdots,~n-1)
\end{align*}
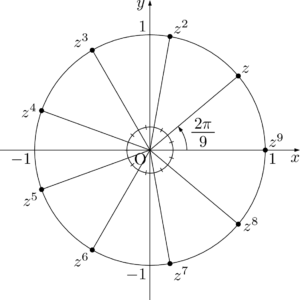
$n=9$ の場合を考えると,$z^9=1$ の解は,
\begin{align*}
z=\cos\dfrac{2k\pi}{9}+i\sin\dfrac{2k\pi}{9}~(k=0,~1,~\cdots,~8)
\end{align*}
と表すことができる。複素数平面上では,次の図のように,点1を1つの頂点とする正九角形の頂点の位置にある。z=\cos\dfrac{2k\pi}{9}+i\sin\dfrac{2k\pi}{9}~(k=0,~1,~\cdots,~8)
\end{align*}
$x^n=1$ の解$x^n=1$ の解は
\begin{align*}
x=\cos\dfrac{2k\pi}{n}+i\sin\dfrac{2k\pi}{n}~(k=0,~1,~2,~\cdots,~n-1)
\end{align*}
となる。複素数平面上では,点1を1つの頂点とする正 $n$ 角形の頂点の位置にある。x=\cos\dfrac{2k\pi}{n}+i\sin\dfrac{2k\pi}{n}~(k=0,~1,~2,~\cdots,~n-1)
\end{align*}
次の式の値を求めよ。
\begin{align*}
&\cos\dfrac{2\pi}{9}+\cos\dfrac{4\pi}{9}+\cos\dfrac{8\pi}{9} \\[4pt]
&\sin\dfrac{\pi}{9}+\sin\dfrac{2\pi}{9}-\sin\dfrac{4\pi}{9}
\end{align*}

ヒロ
上の2つの問題から抜粋しただけなので,答えは既に分かっている。

ヒロ
$\cos\dfrac{2\pi}{9}$ を見たときに,これは $\alpha=\cos\dfrac{2\pi}{9}+i\sin\dfrac{2\pi}{9}$ の実部だなと思うことがある。そして,この $\alpha$ は $\alpha^9=1$ を満たすから,1の9乗根の1つだなぁということも勝手に連想させられる。

ヒロ
こういう発想したからといって,実際に解けるかどうかは分からない。

でも,こういう話をするということは,それで解けるということでもありますね。

ヒロ
まぁそうなる。では,複素数を利用して考えていこう。
\begin{align*}
z=\cos\dfrac{2\pi}{9}+i\sin\dfrac{2\pi}{9}
\end{align*}
とおくと,$z^9=1$ よりz=\cos\dfrac{2\pi}{9}+i\sin\dfrac{2\pi}{9}
\end{align*}
\begin{align*}
&(z^3-1)(z^6+z^3+1)=0
\end{align*}
$z^3\neq1$ であるから&(z^3-1)(z^6+z^3+1)=0
\end{align*}
\begin{align*}
&z^6+z^3+1=0
\end{align*}
この等式の意味は,次の図のように「複素数平面上の3つのベクトルの和が $\vec{0}$ である」と捉えることができる。&z^6+z^3+1=0
\end{align*}
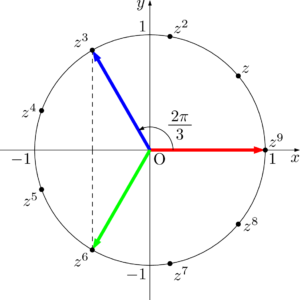
この図だと,3つの複素数は $x^3=1$ の解の配置になっているから,$z^3=\omega$ と表すと,$z^6=\omega^2$, $z^9=\omega^3$ となり,有名な公式 $1+\omega+\omega^2=0$, $\omega^3=1$ が得られる。
1の3乗根$x^3=1$ の3つの解のうち,1でないものの1つを $\omega$ とすると,1でないもう1つの解は $\omega^2$ と表される。また,次の2つの等式が成り立つ。
\begin{align*}
&\omega^3=1 \\[4pt]
&1+\omega+\omega^2=0
\end{align*}
&\omega^3=1 \\[4pt]
&1+\omega+\omega^2=0
\end{align*}
この3つのベクトルを原点のまわりに回転させても,3つのベクトルの和が $\vec{0}$ であることは変わらない。したがって,3つのベクトルを原点のまわりに $\dfrac{2\pi}{9}$ だけ回転させると次のようになる。
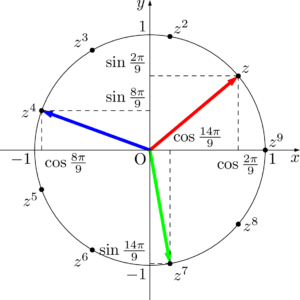
実部に着目すると,

実部に着目すると,
\begin{align*}
\cos\dfrac{2\pi}{9}+\cos\dfrac{8\pi}{9}+\cos\dfrac{14\pi}{9}=0
\end{align*}
が成り立つことが分かる。さらに,$z^7$ の実部は $z^2$ の実部と等しいから\cos\dfrac{2\pi}{9}+\cos\dfrac{8\pi}{9}+\cos\dfrac{14\pi}{9}=0
\end{align*}
\begin{align*}
\cos\dfrac{2\pi}{9}+\cos\dfrac{4\pi}{9}+\cos\dfrac{8\pi}{9}=0
\end{align*}
となる。ちなみに虚部に着目すると\cos\dfrac{2\pi}{9}+\cos\dfrac{4\pi}{9}+\cos\dfrac{8\pi}{9}=0
\end{align*}
\begin{align*}
\sin\dfrac{2\pi}{9}+\sin\dfrac{8\pi}{9}+\sin\dfrac{14\pi}{9}=0
\end{align*}
であることが分かる。さらに変形すると\sin\dfrac{2\pi}{9}+\sin\dfrac{8\pi}{9}+\sin\dfrac{14\pi}{9}=0
\end{align*}
\begin{align*}
\sin\dfrac{2\pi}{9}+\sin\dfrac{\pi}{9}-\sin\dfrac{4\pi}{9}=0
\end{align*}
となる。\sin\dfrac{2\pi}{9}+\sin\dfrac{\pi}{9}-\sin\dfrac{4\pi}{9}=0
\end{align*}

ヒロ
この状態から,3つのベクトルを回転させると,別の等式が得られる。
さらに,原点のまわりに $\dfrac{2\pi}{9}$ だけ回転させると,次のようになる。
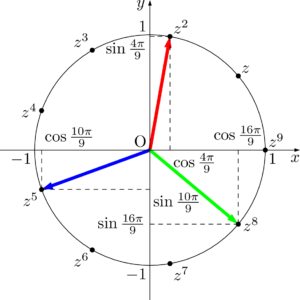
図より,実部に着目すると

図より,実部に着目すると
\begin{align*}
&\cos\dfrac{4\pi}{9}+\cos\dfrac{10\pi}{9}+\cos\dfrac{16\pi}{9}=0 \\[4pt]
&\cos\dfrac{4\pi}{9}-\cos\dfrac{\pi}{9}+\cos\dfrac{2\pi}{9}=0
\end{align*}
が成り立つことが分かる。また,虚部に着目すると&\cos\dfrac{4\pi}{9}+\cos\dfrac{10\pi}{9}+\cos\dfrac{16\pi}{9}=0 \\[4pt]
&\cos\dfrac{4\pi}{9}-\cos\dfrac{\pi}{9}+\cos\dfrac{2\pi}{9}=0
\end{align*}
\begin{align*}
&\sin\dfrac{4\pi}{9}+\sin\dfrac{10\pi}{9}+\sin\dfrac{16\pi}{9}=0 \\[4pt]
&\sin\dfrac{4\pi}{9}-\sin\dfrac{\pi}{9}-\sin\dfrac{2\pi}{9}=0
\end{align*}
が成り立つことも分かる。&\sin\dfrac{4\pi}{9}+\sin\dfrac{10\pi}{9}+\sin\dfrac{16\pi}{9}=0 \\[4pt]
&\sin\dfrac{4\pi}{9}-\sin\dfrac{\pi}{9}-\sin\dfrac{2\pi}{9}=0
\end{align*}


















