Contents
大学入試によく出る三角関数の式の値

ヒロ
上の問題と同じように考えることで,0になる様々な三角関数の式を作ることができる。
$x^9=1$ の9つの解の中の3つ $1,~z^3,~z^6$ から,原点のまわりに $\dfrac{\pi}{9}$ だけ回転した状態を考えると,次の図のようになる。
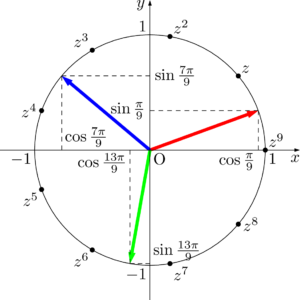
実部と虚部の和はそれぞれ0であるから,次のようになる。
三角関数の公式を使うと,さらに次のように変形できる。

実部と虚部の和はそれぞれ0であるから,次のようになる。
\begin{align*}
&\begin{cases}
\cos\dfrac{\pi}{9}+\cos\dfrac{7\pi}{9}+\cos\dfrac{13\pi}{9}=0 \\[6pt]
\sin\dfrac{\pi}{9}+\sin\dfrac{7\pi}{9}+\sin\dfrac{13\pi}{9}=0
\end{cases}
\end{align*}
度数法で表すと,次のようになる。&\begin{cases}
\cos\dfrac{\pi}{9}+\cos\dfrac{7\pi}{9}+\cos\dfrac{13\pi}{9}=0 \\[6pt]
\sin\dfrac{\pi}{9}+\sin\dfrac{7\pi}{9}+\sin\dfrac{13\pi}{9}=0
\end{cases}
\end{align*}
\begin{align*}
\begin{cases}
\cos20\Deg+\cos140\Deg+\cos260\Deg=0 \\[4pt]
\sin20\Deg+\sin140\Deg+\sin260\Deg=0
\end{cases}
\end{align*}
このように,角度が $120\Deg$ ずつ増えているような式では,正弦・余弦の値の和が0になることは簡単に理解できるだろう。\begin{cases}
\cos20\Deg+\cos140\Deg+\cos260\Deg=0 \\[4pt]
\sin20\Deg+\sin140\Deg+\sin260\Deg=0
\end{cases}
\end{align*}
三角関数の公式を使うと,さらに次のように変形できる。
\begin{align*}
&\begin{cases}
\cos\dfrac{\pi}{9}-\cos\dfrac{2\pi}{9}-\cos\dfrac{4\pi}{9}=0 \\[6pt]
\sin\dfrac{\pi}{9}+\sin\dfrac{2\pi}{9}-\sin\dfrac{4\pi}{9}=0
\end{cases}
\end{align*}
度数法で表すと,次のようになる。&\begin{cases}
\cos\dfrac{\pi}{9}-\cos\dfrac{2\pi}{9}-\cos\dfrac{4\pi}{9}=0 \\[6pt]
\sin\dfrac{\pi}{9}+\sin\dfrac{2\pi}{9}-\sin\dfrac{4\pi}{9}=0
\end{cases}
\end{align*}
\begin{align*}
\begin{cases}
\cos20\Deg-\cos40\Deg-\cos80\Deg=0 \\[4pt]
\sin20\Deg+\sin40\Deg-\sin80\Deg=0
\end{cases}
\end{align*}
この場合は,角度が $120\Deg$ ずつ増えているように見えないため,和が0になることがすぐには分からないから,大学入試としては出題しやすい。\begin{cases}
\cos20\Deg-\cos40\Deg-\cos80\Deg=0 \\[4pt]
\sin20\Deg+\sin40\Deg-\sin80\Deg=0
\end{cases}
\end{align*}

ヒロ
同じようにして,次々と等式を作ることができる。
他には,$10\Deg$ を基準に考えると
\begin{align*}
\cos10\Deg+\cos130\Deg+\cos250\Deg=0
\end{align*}
が成り立つことが分かる。これを変形すると\cos10\Deg+\cos130\Deg+\cos250\Deg=0
\end{align*}
\begin{align*}
\cos10\Deg-\cos50\Deg-\cos70\Deg=0
\end{align*}
が成り立つことも分かる。\cos10\Deg-\cos50\Deg-\cos70\Deg=0
\end{align*}


















