Contents
定積分で面積を求めて6分の1公式を理解しよう

6分の1公式を理解するために,まずは定積分で面積を求める方法を復習しておこう。

2つの曲線 $y=f(x),~y=g(x)$ と $x$ 軸に垂直な2直線 $x=\alpha,~x=\beta$ で囲まれる部分の面積 $S$ を考えよう。
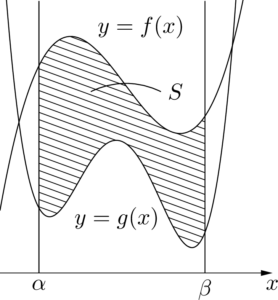
斜線部分の面積 $S$ は次の式で表される。
S&=\dint{\alpha}{\beta}\{f(x)-g(x)\}\;dx
\end{align*}

重要なのはグラフの上下関係と両端の $x$ 座標ということですね。

そうだね。次は具体的に放物線と $x$ 軸で囲まれた部分の面積を考えてみよう。
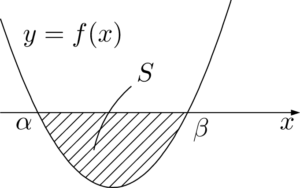
$f(x)=a(x-\alpha)(x-\beta)$ のとき,図の面積 $S$ は次のようになる。
S&=\dint{\alpha}{\beta}\{0-a(x-\alpha)(x-\beta)\}\;dx \\[4pt]
&=-a\dint{\alpha}{\beta}(x-\alpha)(x-\beta)\;dx \\[4pt]
&=\dfrac{1}{6}a(\beta-\alpha)^3
\end{align*}

被積分関数の形と積分区間の関係が重要だよ。

どういうことですか?

例えば,放物線 $C:y=ax^2+bx+c~(a>0)$ と直線 $\ell:y=mx+n$ が2点で交わっていて,その2点の $x$ 座標が $\alpha,\beta$ とする。このとき,$(ax^2+bx+c)-(mx+n)$ を因数分解するとどうなる?

こうなります。
(ax^2+bx+c)-(mx+n)=a(x-\alpha)(x-\beta)
\end{align*}

そうだね。$C$ と $\ell$ で囲まれる部分の面積を $S$ とすると,$a>0$ のとき,$\alpha<x<\beta$ の範囲において,直線 $\ell$ が放物線 $C$ の上側にあるから,面積 $S$ は次のようになる。
S&=\dint{\alpha}{\beta}\{mx+n-(ax^2+bx+c)\}\;dx \\[4pt]
&=-a\dint{\alpha}{\beta}(x-\alpha)(x-\beta)\;dx \\[4pt]
&=\dfrac{1}{6}a(\beta-\alpha)^3
\end{align*}

結局,2つの関数の差が $a(x-\alpha)(x-\beta)$ と因数分解できるから,面積を表す式が同じなんですね。

そういうこと。だから,6分の1公式を使って面積を求めるときは,$x^2$ の係数と2交点の幅に着目すれば良いってことだね。

まとめると次のようになるよ。
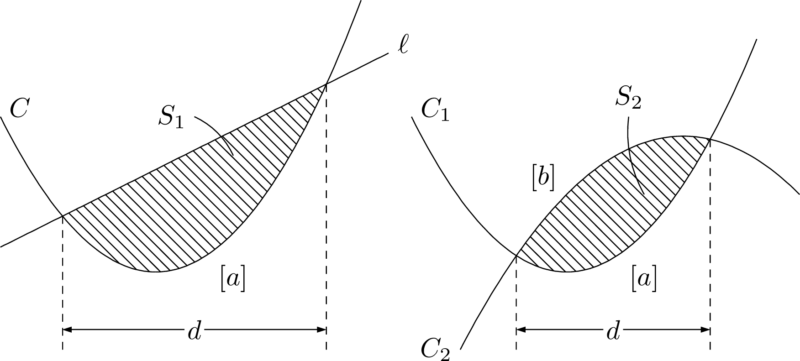
放物線 $C$ と直線 $\ell$ で囲まれた図形の面積を $S_1$ とし,2つの放物線 $C_1,~C_2$ で囲まれた図形の面積を $S_2$ とするとそれぞれ
S_1=\dfrac{1}{6}\abs{a}d^3,~~S_2=\dfrac16(a-b)d^3
\end{align*}

$S_1$ では $C$ が上に凸になっても関係ないように,絶対値にしているよ。

でもこの公式ってあんまり使えないですよね?

確かにこれがそのまま使える問題って教科書の練習問題くらいだね。

だったらこの公式って覚えて使えるようにする意味ってあるんですか?

本当の使い方を知ったら見る目が変わるかもね。


















