Contents
6分の1公式の絶対に知っておくべき使い方

ヒロ
ではもう1問やってみよう。
2011年 群馬大2つの関数 $f(x)=x^2-x$,$g(x)=ax$ がある。
ただし,$a$ は正の定数とする。
$y=\abs{f(x)}$ と $y=g(x)$ のグラフで囲まれる部分の面積を求めよ。
ただし,$a$ は正の定数とする。
$y=\abs{f(x)}$ と $y=g(x)$ のグラフで囲まれる部分の面積を求めよ。

ヒロ
まずはグラフを描こう。別々に描くと次のようになる。
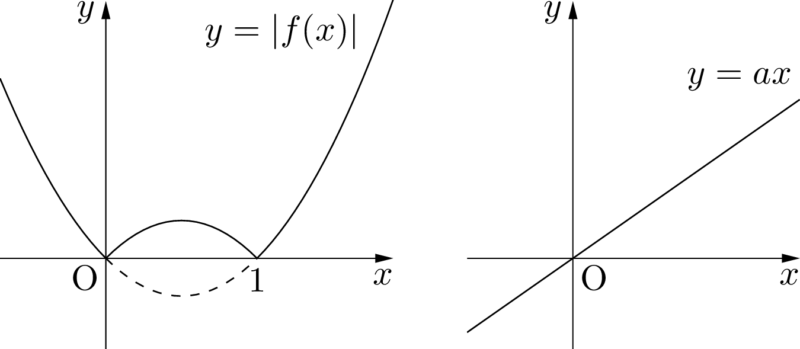

ヒロ
この2つのグラフを1つの $xy$ 平面上に描くときには共有点に注意しよう。
まず,必ず原点が2つのグラフの共有点になっているね。原点以外の共有点は $a$ の値によって変わるため,場合分けが必要となる。

ヒロ
図で表すと次の2つの場合があるね。
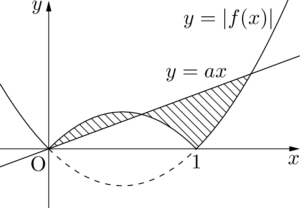
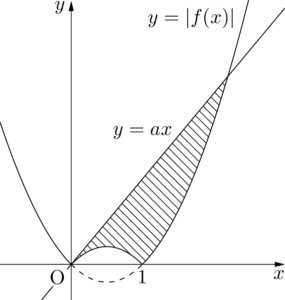

そうですね。図形が変わるので,面積を求める式も違ってきます。

ヒロ
何がこの2つの図の違いになるかを考えよう。

直線 $y=ax$ が原点で接するときの傾きで分ければ良いんじゃないですか?

ヒロ
そうだね。ということで,まずは $y=-x^2+x$ 上にある原点における接線の傾きを求めよう。

$y’=-2x+1$ だから,原点における接線の傾きは,$x=0$ を代入して,1になります。

ヒロ
ということは,$0<a<1$ のときと,$a\geqq1$ のときで場合分けすれば良いってことが分かったね。まずは交点の $x$ 座標を求めよう。
【$0<a<1$ のとき】
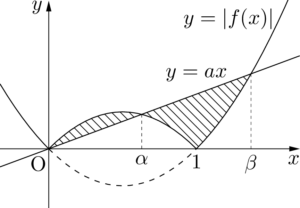
図のように2つの交点の $x$ 座標を $\alpha,\beta$ とする。
$\alpha$ を求める。

図のように2つの交点の $x$ 座標を $\alpha,\beta$ とする。
$\alpha$ を求める。
\begin{align*}
&\begin{cases}
y=-x^2+x \\[4pt]
y=ax
\end{cases} \\[4pt]
&x^2+(a-1)x=0 \\[4pt]
&x\{x+(a-1)\}=0 \\[4pt]
&x=0,1-a \\[4pt]
&\alpha=1-a
\end{align*}
次に $\beta$ を求める。&\begin{cases}
y=-x^2+x \\[4pt]
y=ax
\end{cases} \\[4pt]
&x^2+(a-1)x=0 \\[4pt]
&x\{x+(a-1)\}=0 \\[4pt]
&x=0,1-a \\[4pt]
&\alpha=1-a
\end{align*}
\begin{align*}
&\begin{cases}
y=x^2-x \\[4pt]
y=ax
\end{cases} \\[4pt]
&x^2-(a+1)x=0 \\[4pt]
&x\{x-(a+1)\}=0 \\[4pt]
&x=0,a+1 \\[4pt]
&\beta=a+1
\end{align*}
&\begin{cases}
y=x^2-x \\[4pt]
y=ax
\end{cases} \\[4pt]
&x^2-(a+1)x=0 \\[4pt]
&x\{x-(a+1)\}=0 \\[4pt]
&x=0,a+1 \\[4pt]
&\beta=a+1
\end{align*}

ヒロ
次に面積を求めよう。
\begin{align*}
(左側の面積)&=\dfrac{1}{6}\alpha^3=\dfrac{1}{6}(1-a)^3
\end{align*}
右側の部分の面積を今まで通り定積分で求めると次のようになる。(左側の面積)&=\dfrac{1}{6}\alpha^3=\dfrac{1}{6}(1-a)^3
\end{align*}
\begin{align*}
(右側の面積)&=\dint{\alpha}{1}\{ax-(-x^2+x)\}\;dx+\dint{1}{\beta}\{ax-(x^2-x)\}\;dx \\[4pt]
&=\dint{1-a}{1}\{x^2+(a-1)x\}\;dx+\dint{1}{a+1}\{-x^2+(a+1)x\}\;dx \\[4pt]
&=\Tint{\dfrac{1}{3}x^3+\dfrac{a-1}{2}x^2}{1-a}{1}+\Tint{-\dfrac{1}{3}x^3+\dfrac{a+1}{2}x^2}{1}{a+1} \\[4pt]
&=\dfrac{1}{3}+\dfrac{a-1}{2}-\dfrac{1}{3}(1-a)^3-\dfrac{a-1}{2}(1-a)^2 \\[4pt]
&\hspace{30pt}-\dfrac{1}{3}(a+1)^3+\dfrac{a+1}{2}(a+1)^2+\dfrac{1}{3}-\dfrac{a+1}{2} \\[4pt]
&=\dfrac{1}{6}(1-a)^3+\dfrac{1}{6}(a+1)^3-\dfrac{1}{3} \\[4pt]
&=\dfrac{1}{6}(1-3a+3a^2-a^3)+\dfrac{1}{6}(a^3+3a^2+3a+1)-\dfrac{1}{3} \\[4pt]
&=a^2
\end{align*}
(右側の面積)&=\dint{\alpha}{1}\{ax-(-x^2+x)\}\;dx+\dint{1}{\beta}\{ax-(x^2-x)\}\;dx \\[4pt]
&=\dint{1-a}{1}\{x^2+(a-1)x\}\;dx+\dint{1}{a+1}\{-x^2+(a+1)x\}\;dx \\[4pt]
&=\Tint{\dfrac{1}{3}x^3+\dfrac{a-1}{2}x^2}{1-a}{1}+\Tint{-\dfrac{1}{3}x^3+\dfrac{a+1}{2}x^2}{1}{a+1} \\[4pt]
&=\dfrac{1}{3}+\dfrac{a-1}{2}-\dfrac{1}{3}(1-a)^3-\dfrac{a-1}{2}(1-a)^2 \\[4pt]
&\hspace{30pt}-\dfrac{1}{3}(a+1)^3+\dfrac{a+1}{2}(a+1)^2+\dfrac{1}{3}-\dfrac{a+1}{2} \\[4pt]
&=\dfrac{1}{6}(1-a)^3+\dfrac{1}{6}(a+1)^3-\dfrac{1}{3} \\[4pt]
&=\dfrac{1}{6}(1-3a+3a^2-a^3)+\dfrac{1}{6}(a^3+3a^2+3a+1)-\dfrac{1}{3} \\[4pt]
&=a^2
\end{align*}

結構大変ですね・・・

ヒロ
次のように補助線を描いて,青色と緑色の部分の面積について考えよう。
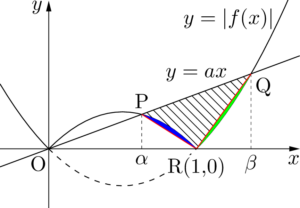
青色と緑色の部分はどちらも放物線と直線で囲まれた部分である。$x^2$ の係数の絶対値はともに1で等しい。
幅を確認すると,青色の部分については,
\begin{align*}
1-\alpha=1-(1-a)=a
\end{align*}
緑色の部分については,1-\alpha=1-(1-a)=a
\end{align*}
\begin{align*}
\beta-1=(a+1)-1=a
\end{align*}
よって,幅も等しいから,2つの面積は等しい。\beta-1=(a+1)-1=a
\end{align*}

ヒロ
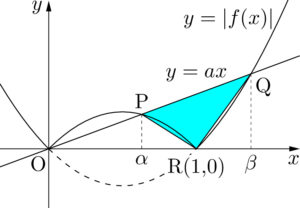
緑色の部分を青色の部分に置き換えると,右側の部分の面積は $\triangle{\mathrm{PQR}}$ の面積に等しくなる。

ヒロ
さらに等積変形によって,次のような三角形の面積を考えれば良いことが分かる。
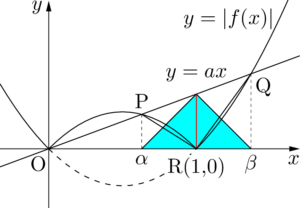
\begin{align*}
(右側の面積)&=\dfrac{1}{2}(\beta-\alpha)\Cdota a \\[4pt]
&=\dfrac{1}{2}\{(a+1)-(1-a)\}a \\[4pt]
&=a^2
\end{align*}
(右側の面積)&=\dfrac{1}{2}(\beta-\alpha)\Cdota a \\[4pt]
&=\dfrac{1}{2}\{(a+1)-(1-a)\}a \\[4pt]
&=a^2
\end{align*}

計算量がかなり少なくなりましたね!

ヒロ
この等積変形は結構有名だから使いこなせるようにしよう!

ヒロ
ということで求める面積 $S$ は次のようになる。
\begin{align*}
S&=\dfrac{1}{6}(1-a)^3+a^2 \\[4pt]
&=-\dfrac{1}{6}a^3+\dfrac{3}{2}a^2-\dfrac{1}{2}a+\dfrac{1}{6}
\end{align*}
S&=\dfrac{1}{6}(1-a)^3+a^2 \\[4pt]
&=-\dfrac{1}{6}a^3+\dfrac{3}{2}a^2-\dfrac{1}{2}a+\dfrac{1}{6}
\end{align*}

ヒロ
では,次は $a\geqq1$ のときを考えよう。
【$a\geqq1$ のとき】
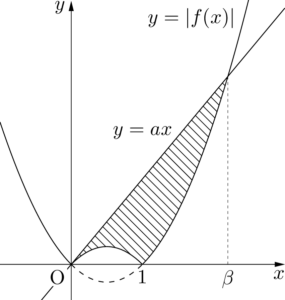


ヒロ
これは6分の1公式をうまく使うことで楽に計算できるね。
\begin{align*}
S&=\dfrac{1}{6}\beta^3-2\times\dfrac{1}{6}\Cdota1^3 \\[4pt]
&=\dfrac{1}{6}(a+1)^3-\dfrac{1}{3} \\[4pt]
&=\dfrac{1}{6}a^3+\dfrac{1}{2}a^2+\dfrac{1}{2}a-\dfrac{1}{6}
\end{align*}
S&=\dfrac{1}{6}\beta^3-2\times\dfrac{1}{6}\Cdota1^3 \\[4pt]
&=\dfrac{1}{6}(a+1)^3-\dfrac{1}{3} \\[4pt]
&=\dfrac{1}{6}a^3+\dfrac{1}{2}a^2+\dfrac{1}{2}a-\dfrac{1}{6}
\end{align*}

図形パズルが得意なら簡単ですね!


















