Contents
6分の1公式の効果的な使い方

まずは簡単な問題で説明していくよ。
\dfrac{\left(\mybox{ア}-\mybox{イ}\right)^{\myBox{ウ}}\left(\myBox{エ}-\myBox{オ}\right)}{\myBox{カ}}
\end{align*}

まずは図を描いてどんな図形なのかを把握しよう。
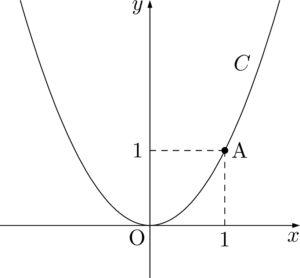

ここまでは良いと思う。直線 $l$ を次のように描いた人は要注意だ。
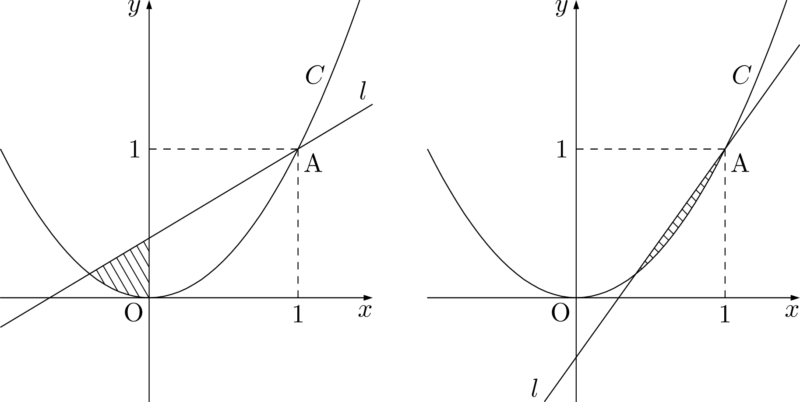

左側は全体の図に対して,今から面積を求めようとしている斜線部分が小さすぎますね。

右側は $l$ と $C$ で囲まれた図形の $x\leqq0$ の部分が存在しませんね。

上図のように描いてしまう人は,文字は常に正だと考えているか,与えられている $l$ の傾きの $a$ の条件を見ずに描いているんだろうね。

なるほど。そうならないように注意します。

問題文では,$a<1$ と定められている。これは,$l$ と $C$ のA以外の交点は $x\leqq0$ の部分にありますよってことを意味する。

原点とAを通るときに,ちょうど傾きが1だから,それより傾きが小さいってことですからね。

傾きが正なんて決められていないのだから,傾きを負にして考える図形が大きくなるようにするべきだね。

ということで次のような図を描こう。
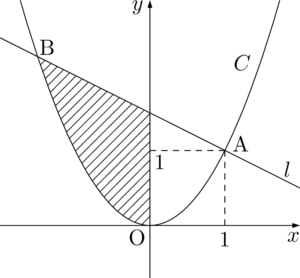

やっぱり6分の1公式は使えないですよ?

そのままでは使えないので,補助線を1本引こう!こんな風に・・・
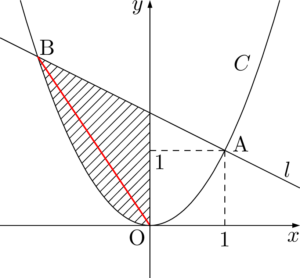

見やすいように色を付けるとこうなる。
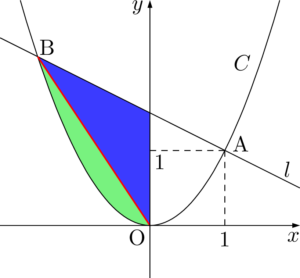

補助線1本で全然違って見えますね!

緑色の方は6分の1公式が使えるし,青色の方はただの三角形だからね。

ということは $C$ と $l$ の2つの交点のうち,Aじゃない方のBの $x$ 座標を求めれば終わりですね。

それはどうやって求める?

連立方程式じゃないんですか?

連立方程式から2次方程式を作るところまでは同じだけど,ここでは,それを普通に解くんじゃなくて,解と係数の関係を使う方法も身に付けておこう。

まぁ,実際にやってみよう。
&x^2-(ax-a+1)=0 \\[4pt]
&x^2-ax+a-1=0
\end{align*}
&b\times1=a-1 \\[4pt]
&b=a-1
\end{align*}

なるほど。結構良いかもしれないですね。

これで面積を求められるね。
(\textcolor[rgb]{0.47,0.95,0.5}{緑色}の部分)&=\dfrac{1}{6}\Cdota1\Cdota(1-a)^3=\dfrac{1}{6}(1-a)^3
\end{align*}
(\textcolor[rgb]{0.23,0.23,1}{青色}の部分)&=\dfrac{1}{2}(1-a)^2
\end{align*}
S&=\dfrac{1}{6}(1-a)^3+\dfrac{1}{2}(1-a)^2 \\[4pt]
&=\dfrac{1}{6}(1-a)^2\{(1-a)+3\} \\[4pt]
&=\dfrac{(1-a)^2(4-a)}{6} \\[4pt]
&=\dfrac{(a-1)^2(4-a)}{6}
\end{align*}
\myBox{ウ}=2,~\myBox{エ}=4,~\myBox{オ}=a,~\myBox{カ}=6
\end{align*}

これは楽ですね!

補助線を引くことで6分の1公式を使えるようにするテクニックを身に付けよう!


















