Contents
- ページ1
- 1 2020年 関西医科大
- ページ2
- 1 2020年 玉川大
- ページ3
- 1 2020年 日本女子大
2020年 日本女子大
2020年 日本女子大次の関数の最小値と最大値,および,そのときの $x$ の値を求めよ。
\begin{align*}
y=\sin^2x+3\cos^2x-2\sqrt{3}\sin x\cos x-2\sqrt{3}\sin x+6\cos x-1~\left(-\dfrac{\pi}{2}\leqq x\leqq\dfrac{7}{6}\pi\right)
\end{align*}
y=\sin^2x+3\cos^2x-2\sqrt{3}\sin x\cos x-2\sqrt{3}\sin x+6\cos x-1~\left(-\dfrac{\pi}{2}\leqq x\leqq\dfrac{7}{6}\pi\right)
\end{align*}
【考え方と解答】
与えられた関数の「$\sin^2x+3\cos^2x-2\sqrt{3}\sin x\cos x$」を見て「$\sin x-\sqrt{3}\cos x=t$」とおくことを考える。このとき,$t^2=\sin^2x+3\cos^2x-2\sqrt{3}\sin x\cos x$ となるから,残りの項を $t$ で表せればうまくいく。
「$-2\sqrt{3}\sin x+6\cos x$」を変形すると
$t=\sin x-\sqrt{3}\cos x$ とおくと
$-\dfrac{\pi}{2}\leqq x\leqq\dfrac{7}{6}\pi$ のとき,$-\dfrac{5}{6}\pi\leqq x-\dfrac{\pi}{3}\leqq\dfrac{5}{6}\pi$ であるから
頂点付近が分かりにくいから,拡大すると次のようになる。ただし,$t$ 軸の位置を変えている。

よって,$t=-2$ のとき最大となり,$t=\sqrt{3}$ のとき最小となる。
$t=-2$ のときの $x$ を求める。
与えられた関数の「$\sin^2x+3\cos^2x-2\sqrt{3}\sin x\cos x$」を見て「$\sin x-\sqrt{3}\cos x=t$」とおくことを考える。このとき,$t^2=\sin^2x+3\cos^2x-2\sqrt{3}\sin x\cos x$ となるから,残りの項を $t$ で表せればうまくいく。
「$-2\sqrt{3}\sin x+6\cos x$」を変形すると
\begin{align*}
-2\sqrt{3}\sin x+6\cos x&=-2\sqrt{3}(\sin x-\sqrt{3}\cos x) \\[4pt]
&=-2\sqrt{3}t
\end{align*}
となり $t$ で表せるから,この方法でうまくいくことが分かる。-2\sqrt{3}\sin x+6\cos x&=-2\sqrt{3}(\sin x-\sqrt{3}\cos x) \\[4pt]
&=-2\sqrt{3}t
\end{align*}
$t=\sin x-\sqrt{3}\cos x$ とおくと
\begin{align*}
t=2\sin\left(x-\dfrac{\pi}{3}\right)
\end{align*}
t=2\sin\left(x-\dfrac{\pi}{3}\right)
\end{align*}

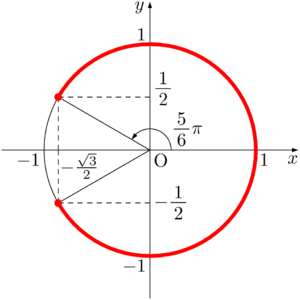
$-\dfrac{\pi}{2}\leqq x\leqq\dfrac{7}{6}\pi$ のとき,$-\dfrac{5}{6}\pi\leqq x-\dfrac{\pi}{3}\leqq\dfrac{5}{6}\pi$ であるから
\begin{align*}
&-1\leqq\sin\left(x-\dfrac{\pi}{3}\right)\leqq1 \\[4pt]
&-2\leqq t\leqq2
\end{align*}
$y$ を $t$ で表すと&-1\leqq\sin\left(x-\dfrac{\pi}{3}\right)\leqq1 \\[4pt]
&-2\leqq t\leqq2
\end{align*}
\begin{align*}
y&=t^2-2\sqrt{3}t-1 \\[4pt]
&=(t-\sqrt{3})^2-4
\end{align*}
y&=t^2-2\sqrt{3}t-1 \\[4pt]
&=(t-\sqrt{3})^2-4
\end{align*}

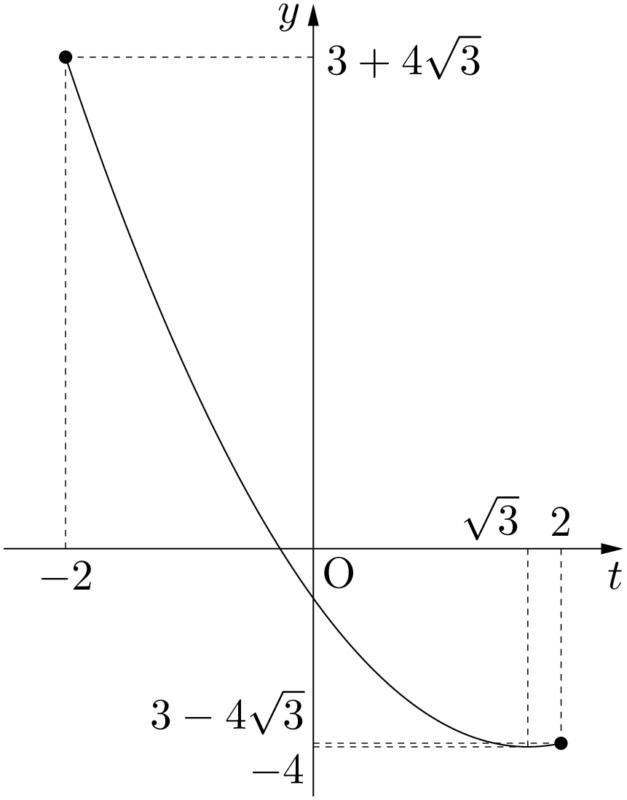
頂点付近が分かりにくいから,拡大すると次のようになる。ただし,$t$ 軸の位置を変えている。

よって,$t=-2$ のとき最大となり,$t=\sqrt{3}$ のとき最小となる。
$t=-2$ のときの $x$ を求める。
\begin{align*}
&\sin\left(x-\dfrac{\pi}{3}\right)=-1 \\[4pt]
&x-\dfrac{\pi}{3}=-\dfrac{\pi}{2} \\[4pt]
&x=-\dfrac{\pi}{6}
\end{align*}
$t=\sqrt{3}$ のときの $x$ を求める。&\sin\left(x-\dfrac{\pi}{3}\right)=-1 \\[4pt]
&x-\dfrac{\pi}{3}=-\dfrac{\pi}{2} \\[4pt]
&x=-\dfrac{\pi}{6}
\end{align*}
\begin{align*}
&\sin\left(x-\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{2} \\[4pt]
&x-\dfrac{\pi}{3}=\dfrac{\pi}{3},~\dfrac{2}{3}\pi \\[4pt]
&x=\dfrac{2}{3}\pi,~\pi
\end{align*}
したがって,$x=-\dfrac{\pi}{6}$ のとき最大値 $3+4\sqrt{3}$ をとり,$x=\dfrac{2}{3}\pi,~\pi$ のとき最小値 $-4$ をとる。&\sin\left(x-\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{2} \\[4pt]
&x-\dfrac{\pi}{3}=\dfrac{\pi}{3},~\dfrac{2}{3}\pi \\[4pt]
&x=\dfrac{2}{3}\pi,~\pi
\end{align*}


















