ここでは,三角関数の最大最小問題について説明します。
三角関数の合成ができるようになると,様々な問題と出会うことになります。
誘導がなくても解けるようにしておくことが重要です。
Contents
- ページ1
- 1 2020年 関西医科大
- ページ2
- 1 2020年 玉川大
- ページ3
- 1 2020年 日本女子大
2020年 関西医科大
2020年 関西医科大$0\leqq\theta\leqq\pi$ のとき,関数 $y=4\sqrt{2}\cos\theta\sin\theta-4\cos\theta-4\sin\theta$ は $\theta=\myhako$ のときに最大値 $\myhako$ をとり,$\theta=\myhako$ のときに最小値 $\myhako$ をとる。
【考え方と解答】
関数が与えられたときは,その関数がどのような特徴をもっているかを考えるようにしよう。今回の場合,与えられた関数は $\sin\theta$ と $\cos\theta$ の対称式になっていることに気付くようにしよう。このことに気付くと,$\sin\theta+\cos\theta$ と $\sin\theta\cos\theta$ で表せることが分かる。
ここで,$\sin\theta+\cos\theta=t$ とおくと,$\sin\theta\cos\theta$ が
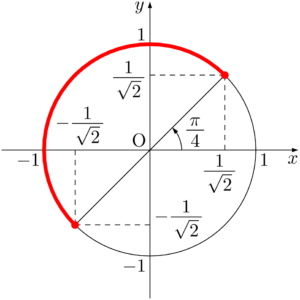
$0\leqq\theta\leqq\pi$ のとき,$\dfrac{\pi}{4}\leqq\theta+\dfrac{\pi}{4}\leqq\dfrac{5}{4}\pi$ であるから,
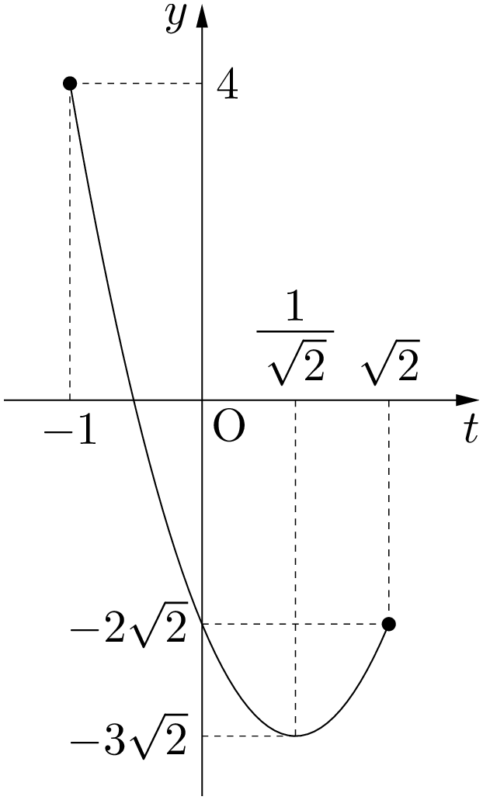
$y$ は $t=-1$ のとき,最大となり,$t=\dfrac{1}{\sqrt{2}}$ のとき,最小となる。$t=-1$ のときの $x$ を求める。
$t=\dfrac{1}{\sqrt{2}}$ のときの $x$ を求める。
したがって,$\theta=\pi$ のとき,最大値4をとり,$\theta=\dfrac{7}{12}\pi$ のとき,最小値 $-3\sqrt{2}$ をとる。
関数が与えられたときは,その関数がどのような特徴をもっているかを考えるようにしよう。今回の場合,与えられた関数は $\sin\theta$ と $\cos\theta$ の対称式になっていることに気付くようにしよう。このことに気付くと,$\sin\theta+\cos\theta$ と $\sin\theta\cos\theta$ で表せることが分かる。
ここで,$\sin\theta+\cos\theta=t$ とおくと,$\sin\theta\cos\theta$ が
\begin{align*}
\sin\theta\cos\theta=\dfrac{t^2-1}{2}
\end{align*}
となることは常識にしておこう。また,文字を置き換えたときには,定義域に注意しよう。合成して調べよう。$t$ を変形すると\sin\theta\cos\theta=\dfrac{t^2-1}{2}
\end{align*}
\begin{align*}
t=\sqrt{2}\sin\left(\theta+\dfrac{\pi}{4}\right)
\end{align*}
となる。t=\sqrt{2}\sin\left(\theta+\dfrac{\pi}{4}\right)
\end{align*}

$0\leqq\theta\leqq\pi$ のとき,$\dfrac{\pi}{4}\leqq\theta+\dfrac{\pi}{4}\leqq\dfrac{5}{4}\pi$ であるから,
\begin{align*}
&-\dfrac{1}{\sqrt{2}}\leqq\sin\left(\theta+\dfrac{\pi}{4}\right)\leqq1 \\[4pt]&-1\leqq t\leqq\sqrt{2}
\end{align*}
$y$ を $t$ で表す。&-\dfrac{1}{\sqrt{2}}\leqq\sin\left(\theta+\dfrac{\pi}{4}\right)\leqq1 \\[4pt]&-1\leqq t\leqq\sqrt{2}
\end{align*}
\begin{align*}
y&=4\sqrt{2}\Cdota\dfrac{t^2-1}{2}-4t \\[4pt]&=2\sqrt{2}t^2-4t-2\sqrt{2} \\[4pt]&=2\sqrt{2}\left(t-\dfrac{1}{\sqrt{2}}\right)^2-3\sqrt{2}
\end{align*}
y&=4\sqrt{2}\Cdota\dfrac{t^2-1}{2}-4t \\[4pt]&=2\sqrt{2}t^2-4t-2\sqrt{2} \\[4pt]&=2\sqrt{2}\left(t-\dfrac{1}{\sqrt{2}}\right)^2-3\sqrt{2}
\end{align*}

$y$ は $t=-1$ のとき,最大となり,$t=\dfrac{1}{\sqrt{2}}$ のとき,最小となる。$t=-1$ のときの $x$ を求める。
\begin{align*}
\sin\left(\theta+\dfrac{\pi}{4}\right)=-\dfrac{1}{\sqrt{2}}
\end{align*}
であるから,$x+\dfrac{\pi}{4}=\dfrac{5}{4}\pi$ より,$x=\pi$\sin\left(\theta+\dfrac{\pi}{4}\right)=-\dfrac{1}{\sqrt{2}}
\end{align*}
$t=\dfrac{1}{\sqrt{2}}$ のときの $x$ を求める。
\begin{align*}
\sin\left(\theta+\dfrac{\pi}{4}\right)=-\dfrac{1}{2}
\end{align*}
であるから,$x+\dfrac{\pi}{4}=\dfrac{5}{6}\pi$ より,$x=\dfrac{7}{12}\pi$\sin\left(\theta+\dfrac{\pi}{4}\right)=-\dfrac{1}{2}
\end{align*}
したがって,$\theta=\pi$ のとき,最大値4をとり,$\theta=\dfrac{7}{12}\pi$ のとき,最小値 $-3\sqrt{2}$ をとる。



















