日常生活でも「○○は必要だ」とか「○○で十分だ」などと言うときがあります。
このような必要条件と十分条件について説明します。
日常生活の必要条件・十分条件と数学でのそれらは異なるという人もいますが,ほとんど同じなので惑わされないようにしましょう。
敢えて違う点を言うなら「必ず」が入るかどうかです。
例えば「大学に合格するためには勉強することが必要だ。」という文章から,「勉強すること」が大学に合格するための必要条件ということができます。
しかし勉強しなくても大学には合格できるということになると,必ずしも勉強することが必要ではなくなります。
他の例では「1日生活するのに1万円あれば十分足りる。」という文章からは,言っている人にとっては1万円あれば1日の生活で特に困ることはないということになります。
しかし1日1万円ではまったく足りないという人もいます。
したがって1万円持っていることは1日生活するための十分条件にはならないということになります。
日常生活ではどんなことでも「必ず」ということはできないため,数学における必要条件とは異なるとなってしまうのでしょう。
日常生活の条件と数学の条件はほとんど同じですが,正確な定義を知っておくのも大切なことです。
必要条件や十分条件などを的確に判断できるようにしておきましょう。
Contents
必要条件と十分条件

まずは必要条件と十分条件の定義を知ることから始めよう。

また $p\Longrightarrow q$,$q\Longrightarrow p$ の両方が成り立つ場合もある。
また,このとき,$p$ と $q$ は互いに同値であるという。
必要条件と十分条件の覚え方

命題 $p\Longrightarrow q$ が真であるときに条件 $p$ が $q$ であるための必要条件なのか十分条件なのか区別が付かなくなる人が多い。

正しく区別できるようになるだけで,得点がアップするのは間違いないので,しっかりできるようにしておこう。
条件 $p,~q$ を満たす要素全体の集合をそれぞれ $P,~Q$ とする。
命題 $p\Longrightarrow q$ が真であるとき「$P$ の要素であればすべて $Q$ の要素である」ことが言えるから,次の図のように集集合 $P$ が集合 $Q$ に含まれる。
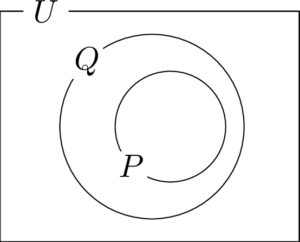
条件 $p$ を満たすことを「$P$ の内部にいる」と表現すると,「$Q$ の内部にいるためには,$P$ の内部にいれば十分である」と言える。
したがって,$p$ は $q$ であるための十分条件である。
逆に「$P$ の内部にいるためには,$Q$ の内部にいることが最低限必要である」と言えるため,$q$ は $p$ であるための必要条件である。

日常生活においても,(最低限)必要(となる)条件を満たす要素は多くなる。逆にこれで十分だという条件を満たす要素は少なくなる。

条件の数が少ないと,これが最低限必要な条件となり,条件の数が多いと,これだけ多くの
条件を満たせば十分だと考えるのが,ごく一般的だと思うが,この条件の数を要素の数と勘違いしてしまうため,訳が分からなくなるのだと思う。

ベン図の集合の大きさは要素の個数を表していると考えることで勘違いを防ぐことができる。

意味を考えれば正しく判断することはできるけど,試験時間が短い試験では機械的に処理をしたい。
例えば次のイラストでは,矢印の先にNが書かれている。

もちろん,このNはnorth(北)を表すNであるが,これをnecessary(必要な)のNと解釈してしまうことで,矢印の先の条件が必要条件だと考えることができる。
また,物流で考えると,物資が十分あるほうから必要なほうへ流れていく。
十分 \Longrightarrow 必要
\end{align*}

これはあくまで一例で,各自の好きなように作って正しく使えれば何も問題はない。

どちらが必要条件を表すかが分かっていても,そもそも命題の真偽を正しく判定できないと何も意味がない。

そのために数学の様々な分野の基礎力を上げよう。
必要条件と十分条件に関する問題

それでは実際に定期テストで出題された問題を解いてみよう。
①必要条件であるが十分条件ではない
②十分条件であるが必要条件ではない
③必要十分条件である
④必要条件でも十分条件でもない
(1) $x=2$ は $2x^2-x-6=0$ であるための $\myhako$。
(2) $x^2=y^2$ は $x=y$ であるための $\myhako$。
(3) $x=y=0$ は $x^2+y^2=0$ であるための $\myhako$。
(4) $\abs{x-3}<2$ は $-1<x<4$ であるための $\myhako$。
(5) $xy>0$ は $\dfrac{y}{x}+\dfrac{x}{y}\geqq2$ であるための $\myhako$。
(6) 四角形ABCDがひし形であることは,四角形ABCDが正方形であるための $\myhako$。

2つ条件について,どちらの方向に成り立つかを調べよう。
(1)の考え方と解答
$x=2$ のとき
2x^2-x-6&=8-2-6 \\[4pt]
&=0
\end{align*}
次に $2x^2-x-6=0 \Longrightarrow x=2$ の真偽を調べる。
&2x^2-x-6=0 \\[4pt]
&(x-2)(2x+3)=0 \\[4pt]
&x=2,~-\dfrac{3}{2}
\end{align*}
したがって,$x=2$ は成り立つ矢印の根本だから,十分条件である。②
(2)の考え方と解答
$x^2=y^2$ のとき
&x^2-y^2=0 \\[4pt]
&(x+y)(x-y)=0 \\[4pt]
&x=y~または x=-y
\end{align*}
次に逆を調べる。
$x=y$ のとき,$x^2=y^2$ となるから真である。
したがって,$x^2=y^2$ は成り立つ矢印の先にあるから,必要条件である。①
(3)の考え方と解答
$x=y=0$ のとき,$x^2=y^2=0$ であり,$x^2+y^2=0$ が成り立つから真である。
次に逆を調べる。
$x,~y$ はともに実数であるから,$x^2$ と $y^2$ はともに0以上である。
$x^2+y^2=0$ となるのは,$x^2=0$ かつ $y^2=0$ となるとき,すなわち $x=y=0$ となるときである。
よって,逆も真である。
したがって,2つの条件は同値であり,必要十分条件である。③
(4)の考え方と解答
$\abs{x-3}<2$ のとき
次に逆を調べる。
$-1<x<4$ を満たす $x$ で $x=0$ を考えると,$1<x<5$ を満たさないから偽である。
したがって,必要条件でも十分条件でもない。④
(5)の考え方と解答
&\dfrac{y}{x}+\dfrac{x}{y}-2 \\[4pt]
&=\dfrac{y^2+x^2-2xy}{xy} \\[4pt]
&=\dfrac{(x-y)^2}{xy}
\end{align*}
よって $xy>0$ のとき $\dfrac{(x-y)^2}{xy}\geqq0$ となるから真である。
次に逆を調べる。
$\dfrac{y}{x}+\dfrac{x}{y}\geqq2$ が成り立つとき,
\dfrac{(x-y)^2}{xy}\geqq0
\end{align*}
したがって,必要十分条件である。③

ちなみに「相加・相乗平均の関係」と言われる不等式を知っていると,すぐに判定できる。
(6)の考え方と解答

ひし形や正方形の定義を知らないと詰むので,しっかり覚えておこう。
四角形ABCDがひし形であっても,正方形であるとはいえないため,偽である。
次に逆を調べる。
すべての正方形はひし形に含まれるため,真である。
したがって,必要条件である。①

意味を考えると,正方形であるためには,最低限,その四角形はひし形でなければ話にならない。つまり,ひし形であることが必要条件だといえる。
必要条件と十分条件に関する問題2
最も適するものを答えよ。ただし,$a,~b$ は実数とする。
&p:a>1~かつ~b>1 \\[4pt]
&q:a+b>2~かつ~(a-1)(b-1)>0
\end{align*}

$p\Longrightarrow q$ と $q\Longrightarrow p$ が成り立つかを順に調べよう。
$p\Longrightarrow q$ の真偽を調べる。
$p$ が成り立つとき,$a$ と $b$ はともに1より大きいから $a+b>2$ となる。また $a-1,~b-1$ はともに正であるから
(a-1)(b-1)>0
\end{align*}
次に $q\Longrightarrow p$ の真偽を調べる。
$a+b>2$ となる $a,~b$ の組み合わせは無限に存在するから $(a-1)(b-1)>0$ から考える。
$a-1$ と $b-1$ の積が正ということは,$a-1$ と $b-1$ が同符号
ということだから,$a$ と $b$ はともに1より大きいか,ともに1より小さいかのどちらかである。
ここで $a+b>2$ を考えることで $a$ と $b$ はともに1より大きいと分かるから,$q\Longrightarrow p$ も真である。
よって,$p$ は $q$ であるための必要十分条件である。



















