Contents
- ページ1
- 1 2020年 関西医科大
- ページ2
- 1 2020年 玉川大
- ページ3
- 1 2020年 日本女子大
2020年 玉川大
2020年 玉川大$x$ の関数 $f(x)$ を
\begin{align*}
f(x)=2\sin^2x-2\sqrt{3}\sin x\cos x-2\sqrt{3}\sin x+2\cos x~(0\leqq x\leqq\pi)
\end{align*}
とする。$t=\sqrt{3}\sin x-\cos x$ とおいて,$f(x)$ を $t$ の式で表すと $f(x)=t^2-\myhako\,t-\myhako$ となる。したがって,$f(x)$ の最大値は $\myhako$,最小値は $\myhako$ である。f(x)=2\sin^2x-2\sqrt{3}\sin x\cos x-2\sqrt{3}\sin x+2\cos x~(0\leqq x\leqq\pi)
\end{align*}
【考え方と解答】
この問題には誘導があるから,誘導通り解き進めよう。$t=\sqrt{3}\sin x-\cos x$ とおくと
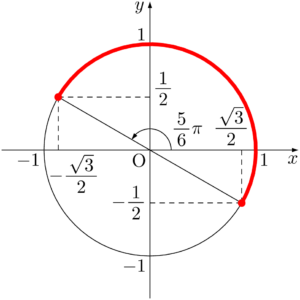
$0\leqq x\leqq\pi$ のとき,$-\dfrac{\pi}{6}\leqq x-\dfrac{\pi}{6}\leqq\dfrac{5}{6}\pi$ であるから
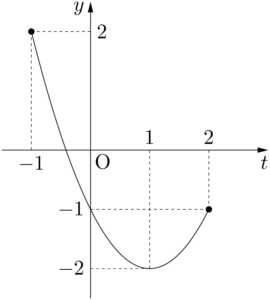
よって,$y$ は $t=-1$ のとき最大値2をとり,$t=1$ のとき最小値 $-2$ をとる。
ちなみに $x$ の値を答える必要はないが,求めると次のようになる。
$t=-1$ のとき
$t=1$ のとき
この問題には誘導があるから,誘導通り解き進めよう。$t=\sqrt{3}\sin x-\cos x$ とおくと
\begin{align*}
t=2\sin\left(x-\dfrac{\pi}{6}\right)
\end{align*}
t=2\sin\left(x-\dfrac{\pi}{6}\right)
\end{align*}

$0\leqq x\leqq\pi$ のとき,$-\dfrac{\pi}{6}\leqq x-\dfrac{\pi}{6}\leqq\dfrac{5}{6}\pi$ であるから
\begin{align*}
&-\dfrac{1}{2}\leqq\sin\left(x-\dfrac{\pi}{6}\right)\leqq1 \\[4pt]
&-1\leqq t\leqq2
\end{align*}
$y$ を $t$ で表す準備として $t^2$ を計算してみる。&-\dfrac{1}{2}\leqq\sin\left(x-\dfrac{\pi}{6}\right)\leqq1 \\[4pt]
&-1\leqq t\leqq2
\end{align*}
\begin{align*}
t^2&=(\sqrt{3}\sin x-\cos x)^2 \\[4pt]
&=3\sin^2x-2\sqrt{3}\sin x\cos x+\cos^2x \\[4pt]
&=2\sin^2x-2\sqrt{3}\sin x\cos x+1
\end{align*}
$y$ を $t$ で表すと次のようになる。t^2&=(\sqrt{3}\sin x-\cos x)^2 \\[4pt]
&=3\sin^2x-2\sqrt{3}\sin x\cos x+\cos^2x \\[4pt]
&=2\sin^2x-2\sqrt{3}\sin x\cos x+1
\end{align*}
\begin{align*}
y&=(2\sin^2x-2\sqrt{3}\sin x\cos x+1)-2(\sqrt{3}\sin x-\cos x)-1 \\[4pt]
&=t^2-2t-1 \\[4pt]
&=(t-1)^2-2
\end{align*}
y&=(2\sin^2x-2\sqrt{3}\sin x\cos x+1)-2(\sqrt{3}\sin x-\cos x)-1 \\[4pt]
&=t^2-2t-1 \\[4pt]
&=(t-1)^2-2
\end{align*}

よって,$y$ は $t=-1$ のとき最大値2をとり,$t=1$ のとき最小値 $-2$ をとる。
ちなみに $x$ の値を答える必要はないが,求めると次のようになる。
$t=-1$ のとき
\begin{align*}
\sin\left(\theta-\dfrac{\pi}{6}\right)=-\dfrac{1}{2}
\end{align*}
であるから,$x-\dfrac{\pi}{6}=-\dfrac{\pi}{6}$ より,$x=0$\sin\left(\theta-\dfrac{\pi}{6}\right)=-\dfrac{1}{2}
\end{align*}
$t=1$ のとき
\begin{align*}
\sin\left(\theta-\dfrac{\pi}{6}\right)=\dfrac{1}{2}
\end{align*}
であるから,\sin\left(\theta-\dfrac{\pi}{6}\right)=\dfrac{1}{2}
\end{align*}
\begin{align*}
&x-\dfrac{\pi}{6}=\dfrac{\pi}{6},~\dfrac{5}{6}\pi \\[4pt]
&x=\dfrac{\pi}{3},~\pi
\end{align*}
&x-\dfrac{\pi}{6}=\dfrac{\pi}{6},~\dfrac{5}{6}\pi \\[4pt]
&x=\dfrac{\pi}{3},~\pi
\end{align*}

ヒロ
誘導がなくても置き換え方が分かるようにしよう。


















