Contents
加法定理を利用して領域を図示する問題
2018年 龍谷大連立不等式
\begin{align*}
\cos(x-y)+\cos(x+y)\geqq0,~0\leqq x\leqq\pi,~0\leqq y\leqq\pi
\end{align*}
の表す領域を座標平面に図示しなさい。\cos(x-y)+\cos(x+y)\geqq0,~0\leqq x\leqq\pi,~0\leqq y\leqq\pi
\end{align*}
【考え方と解答】
加法定理を利用して,与えられた不等式を変形しよう。
$\cos(x-y)+\cos(x+y)\geqq0$ より

加法定理を利用して,与えられた不等式を変形しよう。
$\cos(x-y)+\cos(x+y)\geqq0$ より
\begin{align*}
&\cos x\cos y+\sin x\sin y+\cos x\cos y-\sin x\sin y\geqq0 \\[4pt]
&\cos x\cos y\geqq0 \\[4pt]
&\begin{cases}
\cos x\geqq0 \\[4pt]
\cos y\geqq0
\end{cases}~または~~
\begin{cases}
\cos x\leqq0 \\[4pt]
\cos y\leqq0
\end{cases}
\end{align*}
$0\leqq x\leqq\pi,~0\leqq y\leqq\pi$ より&\cos x\cos y+\sin x\sin y+\cos x\cos y-\sin x\sin y\geqq0 \\[4pt]
&\cos x\cos y\geqq0 \\[4pt]
&\begin{cases}
\cos x\geqq0 \\[4pt]
\cos y\geqq0
\end{cases}~または~~
\begin{cases}
\cos x\leqq0 \\[4pt]
\cos y\leqq0
\end{cases}
\end{align*}
\begin{align*}
&\begin{cases}
0\leqq x\leqq\dfrac{\pi}{2} \\[4pt]
0\leqq y\leqq\dfrac{\pi}{2}
\end{cases}~または~~
\begin{cases}
\dfrac{\pi}{2}\leqq x\leqq\pi \\[4pt]
\dfrac{\pi}{2}\leqq y\leqq\pi
\end{cases}
\end{align*}
よって,求める領域は下図の斜線部分である。ただし,境界を含む。&\begin{cases}
0\leqq x\leqq\dfrac{\pi}{2} \\[4pt]
0\leqq y\leqq\dfrac{\pi}{2}
\end{cases}~または~~
\begin{cases}
\dfrac{\pi}{2}\leqq x\leqq\pi \\[4pt]
\dfrac{\pi}{2}\leqq y\leqq\pi
\end{cases}
\end{align*}

加法定理を利用して三角関数の値を求める問題
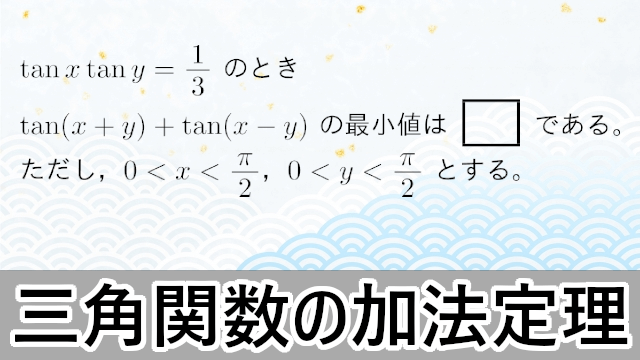
2020年 東海大・医$\tan x\tan y=\dfrac{1}{3}$ のとき $\tan(x+y)+\tan(x-y)$ の最小値は $\myhako$ である。ただし,$0<x<\dfrac{\pi}{2}$,$0<y<\dfrac{\pi}{2}$ とする。
【考え方と解答】
加法定理を用いて $\tan x,~\tan y$ で表してみよう。
このとき,$\tan y=1$ となり,これらを満たす $x,~y$ は①の範囲に存在する。
よって,求める最小値は $\dfrac{3}{2}$ である。
加法定理を用いて $\tan x,~\tan y$ で表してみよう。
\begin{align*}&\tan(x+y)+\tan(x-y) \\[4pt]&=\dfrac{\tan x+\tan y}{1-\tan x\tan y}+\dfrac{\tan x-\tan y}{1+\tan x\tan y} \\[4pt] &=\dfrac{\tan x+\tan y}{1-\dfrac{1}{3}}+\dfrac{\tan x-\tan y}{1+\dfrac{1}{3}} \\[4pt] &=\dfrac{3}{2}(\tan x+\tan y)+\dfrac{3}{4}(\tan x-\tan y) \\[4pt] &=\dfrac{9}{4}\tan x+\dfrac{3}{4}\tan y \end{align*}
「積が一定という条件のもとで最小値を求める」ことを考えると,相加・相乗平均の関係を利用することを考えてみる。 \begin{align*} 0<x<\dfrac{\pi}{2},~0<y<\dfrac{\pi}{2}~\cdots\cdots① \end{align*}
のとき,$\tan x>0,~\tan y>0$ であるから,相加・相乗平均の関係より\begin{align*}
\dfrac{9}{4}\tan x+\dfrac{3}{4}\tan y&\geqq2\sqrt{\dfrac{9}{4}\tan x\Cdota\dfrac{3}{4}\tan y} \\[4pt]
&=\dfrac{3\sqrt{3}}{2}\sqrt{\tan x\tan y} \\[4pt]
&=\dfrac{3\sqrt{3}}{2}\sqrt{\dfrac{1}{3}}=\dfrac{3}{2}
\end{align*}
等号が成り立つのは $\dfrac{9}{4}\tan x=\dfrac{3}{4}\tan y$ となるときである。$\tan x\tan y=\dfrac{1}{3}$ より\dfrac{9}{4}\tan x+\dfrac{3}{4}\tan y&\geqq2\sqrt{\dfrac{9}{4}\tan x\Cdota\dfrac{3}{4}\tan y} \\[4pt]
&=\dfrac{3\sqrt{3}}{2}\sqrt{\tan x\tan y} \\[4pt]
&=\dfrac{3\sqrt{3}}{2}\sqrt{\dfrac{1}{3}}=\dfrac{3}{2}
\end{align*}
\begin{align*}
&\tan x\Cdota3\tan x=\dfrac{1}{3} \\[4pt]
&\tan^2x=\dfrac{1}{9}
\end{align*}
$\tan x>0$ より,$\tan x=\dfrac{1}{3}$&\tan x\Cdota3\tan x=\dfrac{1}{3} \\[4pt]
&\tan^2x=\dfrac{1}{9}
\end{align*}
このとき,$\tan y=1$ となり,これらを満たす $x,~y$ は①の範囲に存在する。
よって,求める最小値は $\dfrac{3}{2}$ である。