ここでは10進数の整数をn進数に変換する方法を説明します。
意味を全く考えずに変換方法だけを知って,問題を解けるようになったとしてもしんどいでしょう。
一般的に,意味が分からないものを覚え続けることは難しいため,3か月もすれば変換方法を忘れてしまうでしょう。
したがって,変換方法の意味を知ることで「忘れたら解けなくなる」という恐怖から解放されるため,逆に変換方法を忘れることがなくなり,解ける問題も増えるでしょう。
10進数を2進数や3進数に変換する問題
2019年 龍谷大10進法で表すと89となる数を2進法と3進法でそれぞれ表しなさい。
【考え方と解答】
2進法で表す場合は,2の累乗の和で表すことを考える。2の累乗のうち,89以下の最大のものは $2^6=64$ である。
2進法で表す場合は,2の累乗の和で表すことを考える。2の累乗のうち,89以下の最大のものは $2^6=64$ である。
\begin{align*}
89&=64+25 \\[4pt]
&=2^6+16+8+1 \\[4pt]
&=2^6+2^4+2^3+1 \\[4pt]
&=1011001_{(2)}
\end{align*}
3進法で表す場合は,3の累乗の和で表すことを考える。89&=64+25 \\[4pt]
&=2^6+16+8+1 \\[4pt]
&=2^6+2^4+2^3+1 \\[4pt]
&=1011001_{(2)}
\end{align*}
\begin{align*}
89&=81+8 \\[4pt]
&=3^4+2\times3+2 \\[4pt]
&=10022_{(3)}
\end{align*}
89&=81+8 \\[4pt]
&=3^4+2\times3+2 \\[4pt]
&=10022_{(3)}
\end{align*}

ヒロ
教科書などに載っている方法でも解いておこう。
【別の考え方と解答】
10進数の89を2進法で表す場合,89を2で割って商と余りを求めていく。商が0になったら,出てきた余りを逆に並べることで2進法で表すことができる。実際に計算すると次のようになる。

この計算より,$89=1011001_{(2)}$
同じように89を3進法で表そう。

この計算より,$89=10022_{(3)}$
10進数の89を2進法で表す場合,89を2で割って商と余りを求めていく。商が0になったら,出てきた余りを逆に並べることで2進法で表すことができる。実際に計算すると次のようになる。

この計算より,$89=1011001_{(2)}$
同じように89を3進法で表そう。

この計算より,$89=10022_{(3)}$

ヒロ
この方法の意味については次の記事で説明しているから,意味を知りたい人は参考にして欲しい。
10進数を7進数に変換する問題
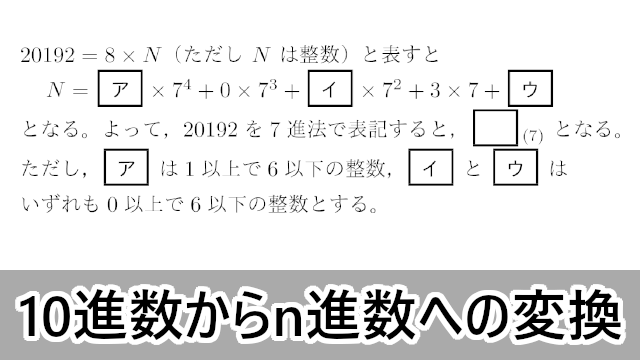
2019年 立命館大・改題$20192=8\times N$(ただし $N$ は整数)と表すと
ただし,$\myBox{ア}$ は1以上で6以下の整数,$\myBox{イ}$ と $\myBox{ウ}$ はいずれも0以上で6以下の整数とする。
\begin{align*}
N=\myBox{ア}\times7^4+0\times7^3+\myBox{イ}\times7^2+3\times7+\myBox{ウ}
\end{align*}
となる。よって,20192を7進法で表記すると,$\myhako_{(7)}$ となる。N=\myBox{ア}\times7^4+0\times7^3+\myBox{イ}\times7^2+3\times7+\myBox{ウ}
\end{align*}
ただし,$\myBox{ア}$ は1以上で6以下の整数,$\myBox{イ}$ と $\myBox{ウ}$ はいずれも0以上で6以下の整数とする。
【考え方と解答】
まずは $20192\div8$ を計算して $N$ を求めよう。
まずは $20192\div8$ を計算して $N$ を求めよう。
\begin{align*}
N=\dfrac{20192}{8}=2524
\end{align*}
次に2524を7の累乗の和で表そう。$7^4=2401$ であるからN=\dfrac{20192}{8}=2524
\end{align*}
\begin{align*}
2524&=2401+123 \\[4pt]
&=7^4+98+21+4 \\[4pt]
&=7^4+2\times7^2+3\times7+4
\end{align*}
この結果を利用して20192を7進法で表そう。2524&=2401+123 \\[4pt]
&=7^4+98+21+4 \\[4pt]
&=7^4+2\times7^2+3\times7+4
\end{align*}
\begin{align*}
20192&=8(7^4+2\times7^2+3\times7+4) \\[4pt]
&=(7+1)(7^4+2\times7^2+3\times7+4) \\[4pt]
&=7^5+7^4+2\times7^3+6\times7^2+4
\end{align*}
よって,20192を7進法で表記すると,$112604_{(7)}$ となる。20192&=8(7^4+2\times7^2+3\times7+4) \\[4pt]
&=(7+1)(7^4+2\times7^2+3\times7+4) \\[4pt]
&=7^5+7^4+2\times7^3+6\times7^2+4
\end{align*}