Contents
三角関数の加法定理の導出

ヒロ
余弦定理を利用して加法定理を導出しよう。
【加法定理の導出】
原点を中心とする単位円周上に,$x$ 軸を始線として,角が $\alpha,~\beta$ である2点P,Qをとる。
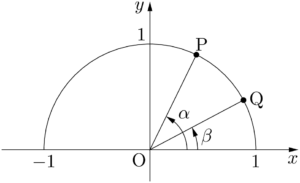
2点P,Qの座標はそれぞれ
①において,$\beta$ を $-\beta$ とおくと
原点を中心とする単位円周上に,$x$ 軸を始線として,角が $\alpha,~\beta$ である2点P,Qをとる。

2点P,Qの座標はそれぞれ
\begin{align*}
\text{P}(\cos\alpha,~\sin\alpha),~\text{Q}(\cos\beta,~\sin\beta)
\end{align*}
となるから,\text{P}(\cos\alpha,~\sin\alpha),~\text{Q}(\cos\beta,~\sin\beta)
\end{align*}
\begin{align*}
\text{PQ}^2&=(\cos\alpha-\cos\beta)^2+(\sin\alpha-\sin\beta)^2 \\[4pt]
&=(\cos^2\alpha+\sin^2\alpha)-2(\cos\alpha\cos\beta+\sin\alpha\sin\beta)+(\cos^2\beta+\sin^2\beta) \\[4pt]
&=2-2(\cos\alpha\cos\beta+\sin\alpha\sin\beta)
\end{align*}
また,$\kaku{POQ}=\alpha-\beta$ であるから,$\sankaku{OPQ}$ において余弦定理を適用すると\text{PQ}^2&=(\cos\alpha-\cos\beta)^2+(\sin\alpha-\sin\beta)^2 \\[4pt]
&=(\cos^2\alpha+\sin^2\alpha)-2(\cos\alpha\cos\beta+\sin\alpha\sin\beta)+(\cos^2\beta+\sin^2\beta) \\[4pt]
&=2-2(\cos\alpha\cos\beta+\sin\alpha\sin\beta)
\end{align*}
\begin{align*}
&\text{PQ}^2=\text{OP}^2+\text{OQ}^2-2\Cdota\text{OP}\Cdota\text{OQ}\cos\kaku{POQ} \\[4pt]
&2-2(\cos\alpha\cos\beta+\sin\alpha\sin\beta)=1+1-2\cos(\alpha-\beta) \\[4pt]
&\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta~\cdots\cdots①
\end{align*}
文字の置き換えを利用して,他の公式を導く。&\text{PQ}^2=\text{OP}^2+\text{OQ}^2-2\Cdota\text{OP}\Cdota\text{OQ}\cos\kaku{POQ} \\[4pt]
&2-2(\cos\alpha\cos\beta+\sin\alpha\sin\beta)=1+1-2\cos(\alpha-\beta) \\[4pt]
&\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta~\cdots\cdots①
\end{align*}
①において,$\beta$ を $-\beta$ とおくと
\begin{align*}
\cos(\alpha+\beta)&=\cos\alpha\cos(-\beta)+\sin\alpha\sin(-\beta) \\[4pt]
&=\cos\alpha\cos\beta-\sin\alpha\sin\beta~\cdots\cdots②
\end{align*}
「グラグラするとかしないとか」を利用して $\cos$ を $\sin$ に変えて,サインの加法定理を導く。②において,$\beta$ を $\beta-\dfrac{\pi}{2}$ とおくと\cos(\alpha+\beta)&=\cos\alpha\cos(-\beta)+\sin\alpha\sin(-\beta) \\[4pt]
&=\cos\alpha\cos\beta-\sin\alpha\sin\beta~\cdots\cdots②
\end{align*}
\begin{align*}
&\cos\left(\alpha+\beta-\dfrac{\pi}{2}\right)=\cos\alpha\cos\left(\beta-\dfrac{\pi}{2}\right)-\sin\alpha\sin\left(\beta-\dfrac{\pi}{2}\right) \\[4pt]
&\sin(\alpha+\beta)=\cos\alpha\sin\beta-\sin\alpha\Cdota(-\cos\beta) \\[4pt]
&\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta~\cdots\cdots③
\end{align*}
③において,$\beta$ を $-\beta$ に置き換えて&\cos\left(\alpha+\beta-\dfrac{\pi}{2}\right)=\cos\alpha\cos\left(\beta-\dfrac{\pi}{2}\right)-\sin\alpha\sin\left(\beta-\dfrac{\pi}{2}\right) \\[4pt]
&\sin(\alpha+\beta)=\cos\alpha\sin\beta-\sin\alpha\Cdota(-\cos\beta) \\[4pt]
&\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta~\cdots\cdots③
\end{align*}
\begin{align*}
\sin(\alpha-\beta)&=\sin\alpha\cos(-\beta)+\cos\alpha\sin(-\beta) \\[4pt]
&=\sin\alpha\cos\beta-\cos\alpha\sin\beta~\cdots\cdots④
\end{align*}
\sin(\alpha-\beta)&=\sin\alpha\cos(-\beta)+\cos\alpha\sin(-\beta) \\[4pt]
&=\sin\alpha\cos\beta-\cos\alpha\sin\beta~\cdots\cdots④
\end{align*}

ヒロ
タンジェントの加法定理の導出については「2009年岩手大の入試問題」の解説記事と重複するため,ここでは省略する。
加法定理と恒等式に関する問題
2018年 岡山理科大関数
\begin{align*}
P(x)=\sin x+\sin(x+a)+\sin(x-a)
\end{align*}
について,次の問いに答えよ。ただし,$0\leqq x\leqq\pi$,$0\leqq a<\pi$ である。 すべての $x$ に対して $P(x)=0$ となる $a$ の値を求めよ。P(x)=\sin x+\sin(x+a)+\sin(x-a)
\end{align*}
【考え方と解答】
加法定理を利用して,$x$ と $a$ を分離しよう。
加法定理を利用して,$x$ と $a$ を分離しよう。
\begin{align*} P(x)&=\sin x+\sin(x+a)+\sin(x-a) \\[4pt] &=\sin x+\sin x\cos a+\cos x\sin a+\sin x\cos a-\cos x\sin a \\[4pt] &=\sin x(1+2\cos a) \end{align*}
すべての $x$ に対して $P(x)=0$ となるのは,$1+2\cos a=0$ が成り立つときであるから,\begin{align*} &\cos a=-\dfrac{1}{2} \end{align*}
$0\leqq a<\pi$ より,$a=\dfrac{2}{3}\pi$