ここでは,2直線のなす角について説明します。
サイン・コサイン・タンジェントの中で,直線の方程式と最も関連あるものはタンジェントである。
したがって,2直線のなす角を考えるときもタンジェントに着目するのが良い。
どのように考えて,2直線のなす角を求めるのかを理解して問題を解けるようにしましょう。
Contents
直線の傾きとタンジェント

ヒロ
直線の方程式が与えられたときは,その直線と $x$ 軸の正の方向となす角のタンジェントが与えられていることと同じである。
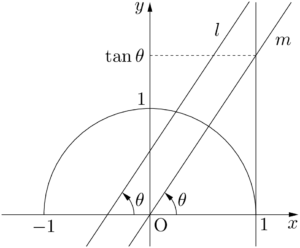
直線の傾きとタンジェント直線 $l:y=ax+b$ と $x$ 軸のなす角を $\theta~(0\leqq\theta\leqq\pi)$ とすると,
原点を通り,直線 $l$ と平行な直線を $m$ とする。直線 $m$ と直線 $x=1$ の交点をPとすると,Pの $y$ 座標は $\tan\theta$ である。したがって,直線 $l$ の傾き $a$ も $\tan\theta$ となり,$a=\tan\theta$ が成り立つ。
\begin{align*}
a=\tan\theta
\end{align*}
が成り立つ。a=\tan\theta
\end{align*}
原点を通り,直線 $l$ と平行な直線を $m$ とする。直線 $m$ と直線 $x=1$ の交点をPとすると,Pの $y$ 座標は $\tan\theta$ である。したがって,直線 $l$ の傾き $a$ も $\tan\theta$ となり,$a=\tan\theta$ が成り立つ。



















