Contents
三角形の面積に関する問題【津田塾大】
2009年 津田塾大(1) 座標平面上に原点O以外の異なる2点P$(x_1,~y_1)$,Q$(x_2,~y_2)$ がある。$\sankaku{OPQ}$ の面積は $\dfrac{1}{2}\abs{x_1y_2-x_2y_1}$ で表されることを示せ。
(2) (1)のP,Qとは異なる点をR$(x_3,~y_3)$ とする。$\sankaku{PQR}$ の面積をP,Q,Rの座標を用いて表せ。
(3) A$(0,~2)$,B$(4,~0)$ とする。$\sankaku{ABC}$ の面積が3,$\kaku{ACB}=90\Deg$ となる点Cの座標をすべて求めよ。
(2) (1)のP,Qとは異なる点をR$(x_3,~y_3)$ とする。$\sankaku{PQR}$ の面積をP,Q,Rの座標を用いて表せ。
(3) A$(0,~2)$,B$(4,~0)$ とする。$\sankaku{ABC}$ の面積が3,$\kaku{ACB}=90\Deg$ となる点Cの座標をすべて求めよ。
【(1)の考え方と解答】
点Qから直線OPに下ろした垂線の長さを $h$ とする。
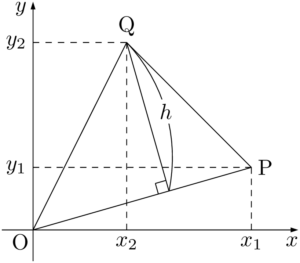
OPの長さは
点Qから直線OPに下ろした垂線の長さを $h$ とする。

OPの長さは
\begin{align*}
\text{OP}=\sqrt{{x_1}^2+{y_1}^2}
\end{align*}
であり,直線OPの方程式は $y_1x-x_1y=0$ であるから $h$ は\text{OP}=\sqrt{{x_1}^2+{y_1}^2}
\end{align*}
\begin{align*}
h=\dfrac{\abs{y_1x_2-x_1y_2}}{\sqrt{{x_1}^2+{y_1}^2}}
\end{align*}
よって,三角形OPQの面積はh=\dfrac{\abs{y_1x_2-x_1y_2}}{\sqrt{{x_1}^2+{y_1}^2}}
\end{align*}
\begin{align*}
\sankaku{OPQ}&=\dfrac{1}{2}\Cdota\text{OP}\Cdota h \\[4pt]
&=\dfrac{1}{2}\Cdota\sqrt{{x_1}^2+{y_1}^2}\Cdota\dfrac{\abs{y_1x_2-x_1y_2}}{\sqrt{{x_1}^2+{y_1}^2}} \\[4pt]
&=\dfrac{1}{2}\abs{x_1y_2-x_2y_1}
\end{align*}
\sankaku{OPQ}&=\dfrac{1}{2}\Cdota\text{OP}\Cdota h \\[4pt]
&=\dfrac{1}{2}\Cdota\sqrt{{x_1}^2+{y_1}^2}\Cdota\dfrac{\abs{y_1x_2-x_1y_2}}{\sqrt{{x_1}^2+{y_1}^2}} \\[4pt]
&=\dfrac{1}{2}\abs{x_1y_2-x_2y_1}
\end{align*}
(2) (1)のP,Qとは異なる点をR$(x_3,~y_3)$ とする。$\sankaku{PQR}$ の面積をP,Q,Rの座標を用いて表せ。
【(2)の考え方と解答】
原点と異なる3点が与えられたときは,3点のうち1つの点が原点に重なるように平行移動させて考えよう。三角形を平行移動させても,その面積は当然変わらないだけでなく,1点が原点に重なることで,(1)の結果を利用できるようになる。どの点が原点に重なるようにするかは好みの問題である。今回は点Rが原点に重なるように平行移動する。
点Rが原点に重なるように $\sankaku{PQR}$ を平行移動したとき,2点P,QがそれぞれS,Tに移ったとすると
原点と異なる3点が与えられたときは,3点のうち1つの点が原点に重なるように平行移動させて考えよう。三角形を平行移動させても,その面積は当然変わらないだけでなく,1点が原点に重なることで,(1)の結果を利用できるようになる。どの点が原点に重なるようにするかは好みの問題である。今回は点Rが原点に重なるように平行移動する。
点Rが原点に重なるように $\sankaku{PQR}$ を平行移動したとき,2点P,QがそれぞれS,Tに移ったとすると
\begin{align*}
\text{S}(x_1-x_3,~y_1-y_3),~\text{T}(x_2-x_3,~y_2-y_3)
\end{align*}
となる。$\sankaku{PQR}$ の面積は $\sankaku{OST}$ の面積に等しいから,(1)の結果より\text{S}(x_1-x_3,~y_1-y_3),~\text{T}(x_2-x_3,~y_2-y_3)
\end{align*}
\begin{align*}
\sankaku{PQR}=\dfrac{1}{2}\abs{(x_1-x_3)(y_2-y_3)-(x_2-x_3)(y_1-y_3)}
\end{align*}
\sankaku{PQR}=\dfrac{1}{2}\abs{(x_1-x_3)(y_2-y_3)-(x_2-x_3)(y_1-y_3)}
\end{align*}
(3) A$(0,~2)$,B$(4,~0)$ とする。$\sankaku{ABC}$ の面積が3,$\kaku{ACB}=90\Deg$ となる点Cの座標をすべて求めよ。
【(3)の考え方と解答】
2つの未知数を用いて点Cの座標を表したとすると,2本の方程式が必要となる。(2)を利用することを考えると,1本の方程式が得られる。もう1本は $\kaku{ACB}=90\Deg$ から得られる。
C$(p,~q)$ とおくと,(2)の結果より
2つの未知数を用いて点Cの座標を表したとすると,2本の方程式が必要となる。(2)を利用することを考えると,1本の方程式が得られる。もう1本は $\kaku{ACB}=90\Deg$ から得られる。
C$(p,~q)$ とおくと,(2)の結果より
\begin{align*}
&\dfrac{1}{2}\abs{pq-(p-4)(q-2)}=3 \\[4pt]
&\dfrac{1}{2}\abs{2p+4q-8}=3 \\[4pt]
&\abs{p+2q-4}=3 \\[4pt]
&p+2q-4=\pm3 \\[4pt]
&p+2q-7=0~\cdots\cdots①~または~p+2q-1=0~\cdots\cdots②
\end{align*}
①より,C$(-2q+7,~q)$ と表せる。$\kaku{ACB}=90\Deg$ より&\dfrac{1}{2}\abs{pq-(p-4)(q-2)}=3 \\[4pt]
&\dfrac{1}{2}\abs{2p+4q-8}=3 \\[4pt]
&\abs{p+2q-4}=3 \\[4pt]
&p+2q-4=\pm3 \\[4pt]
&p+2q-7=0~\cdots\cdots①~または~p+2q-1=0~\cdots\cdots②
\end{align*}
\begin{align*}
&\dfrac{q-2}{-2q+7}\Cdota\dfrac{q}{-2q+3}=-1~\cdots\cdots③ \\[4pt]
&q^2-2q=-4q^2+20q-21 \\[4pt]
&5q^2-22q+21=0 \\[4pt]
&(q-3)(5q-7)=0 \\[4pt]
&q=3,~\dfrac{7}{5}
\end{align*}
②より,C$(-2q+1,~q)$ と表せる。$\kaku{ACB}=90\Deg$ より&\dfrac{q-2}{-2q+7}\Cdota\dfrac{q}{-2q+3}=-1~\cdots\cdots③ \\[4pt]
&q^2-2q=-4q^2+20q-21 \\[4pt]
&5q^2-22q+21=0 \\[4pt]
&(q-3)(5q-7)=0 \\[4pt]
&q=3,~\dfrac{7}{5}
\end{align*}
\begin{align*}
&\dfrac{q-2}{-2q+1}\Cdota\dfrac{q}{-2q-3}=-1~\cdots\cdots④ \\[4pt]
&q^2-2q=-4q^2-4q+3 \\[4pt]
&5q^2+2q-3=0 \\[4pt]
&(q+1)(5q-3)=0 \\[4pt]
&q=-1,~\dfrac{3}{5}
\end{align*}
以上より,求める点Cの座標は&\dfrac{q-2}{-2q+1}\Cdota\dfrac{q}{-2q-3}=-1~\cdots\cdots④ \\[4pt]
&q^2-2q=-4q^2-4q+3 \\[4pt]
&5q^2+2q-3=0 \\[4pt]
&(q+1)(5q-3)=0 \\[4pt]
&q=-1,~\dfrac{3}{5}
\end{align*}
\begin{align*}
(1,~3),~\left(\dfrac{21}{5},~\dfrac{7}{5}\right),~(3,~-1),~\left(-\dfrac{1}{5},~\dfrac{3}{5}\right)
\end{align*}
(1,~3),~\left(\dfrac{21}{5},~\dfrac{7}{5}\right),~(3,~-1),~\left(-\dfrac{1}{5},~\dfrac{3}{5}\right)
\end{align*}

ヒロ
少し補足説明をしておく。
【補足説明】
「③や④の分母が0になるようなときを考慮しなくて良いのか」と思った人は優秀だろう。実際の入試で,上の解答を書いた場合,分母が0になる可能性に触れていないため,減点されるかもしれない。減点されても最後まで答案を仕上げることが重要だと考えた場合は放置すれば良いし,減点されると困るというのであれば,しっかり書けば良い。
しっかり答案を書く方法としては,主に3つある。
- ③や④の分母が0になるときは条件を満たさないことを示す
- 条件を満たす点Cは4つしか存在しないことを説明する
- そもそも分母に文字式が現れないように書く
まず,1つ目の方法から説明する。分母が0になるときは,ACやBCが座標軸と平行になるときであり,その場合は $\kaku{ACB}=90\Deg$ とならないことを示せば良い。
次に,2つ目の方法では,$\kaku{ACB}=90\Deg$ となるような点Cは線分ABを直径とする円周上の点であることを利用して説明することが考えられる。①と②は点Cが直線①や直線②上にあることを示しているから,条件を満たす点Cは下図のように4点しかないことが分かる。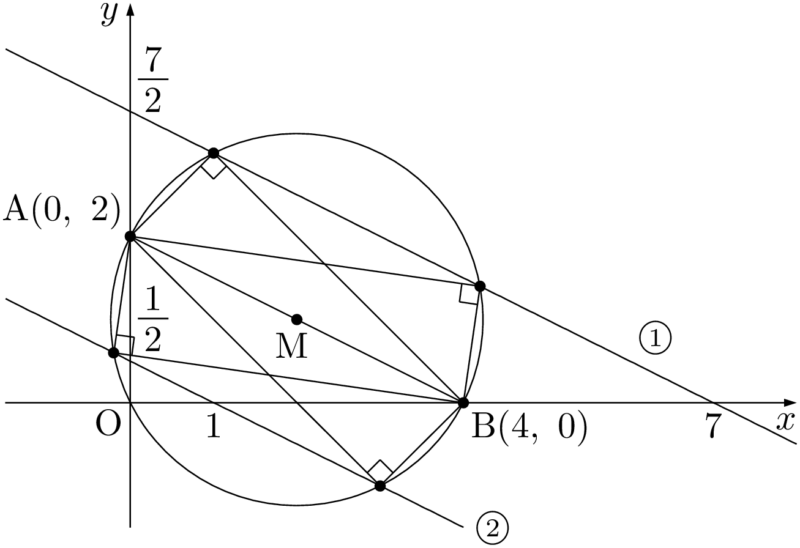
最後の方法は,「ベクトル」を使うことで,そもそも分母に文字が現れないように書くことができる。考え方もそれほど難しくないため,垂直条件や平行条件を扱う際にはベクトルを利用すると良いだろう。
三角形の面積に関する問題【京都薬科大】
2010年 京都薬科大平面上における点Aが直線 $y=2x$ 上を動くとき,点B$(3,~2)$,点C$(5,~7)$ とすると,$\sankaku{ABC}$ の面積が10となるのは,点Aの座標が $\left(\myBox{ア},~\myhako\right)$ または,$\left(\myBox{イ},~\myhako\right)$ のときである。ただし,$\myBox{ア}<\myBox{イ}$ とする。
【考え方と解答】
$\sankaku{ABC}$ の3辺のうち,辺BCの長さは変わらないから,辺BCを底辺とみる。その長さは
直線BCの傾きは
$\sankaku{ABC}$ の3辺のうち,辺BCの長さは変わらないから,辺BCを底辺とみる。その長さは
\begin{align*}
\text{BC}&=\sqrt{(5-3)^2+(7-2)^2} \\[4pt]
&=\sqrt{29}
\end{align*}
$\sankaku{ABC}$ の面積が10になるときを考えるから,高さ $h$ が決まる。\text{BC}&=\sqrt{(5-3)^2+(7-2)^2} \\[4pt]
&=\sqrt{29}
\end{align*}
\begin{align*}
&\dfrac{1}{2}\Cdota\text{BC}\Cdota h=10 \\[4pt]
&\sqrt{29}h=20 \\[4pt]
&h=\dfrac{20}{\sqrt{29}}
\end{align*}
点Aと直線BCとの距離 $d$ が $h$ であることから点Aの座標を求めよう。点Aは直線 $y=2x$ 上の点であるから,1つの文字 $t$ を用いて,座標を表すことができる。つまり,$d=h$ を $t$ を用いて表すことで $t$ の方程式になるから,それを解くことで $t$ を求めることができる。&\dfrac{1}{2}\Cdota\text{BC}\Cdota h=10 \\[4pt]
&\sqrt{29}h=20 \\[4pt]
&h=\dfrac{20}{\sqrt{29}}
\end{align*}
直線BCの傾きは
\begin{align*}
\dfrac{7-2}{5-3}=\dfrac{5}{2}
\end{align*}
であるから,直線BCの方程式は\dfrac{7-2}{5-3}=\dfrac{5}{2}
\end{align*}
\begin{align*}
&y=\dfrac{5}{2}(x-3)+2 \\[4pt]
&2y=5(x-3)+4 \\[4pt]
&5x-2y-11=0
\end{align*}
点Aの座標は $(t,~2t)$ と表せるから,点Aと直線BCとの距離 $d$ は&y=\dfrac{5}{2}(x-3)+2 \\[4pt]
&2y=5(x-3)+4 \\[4pt]
&5x-2y-11=0
\end{align*}
\begin{align*}
d&=\dfrac{\abs{5t-2\Cdot2t-11}}{\sqrt{5^2+(-2)^2}} \\[4pt]
&=\dfrac{\abs{t-11}}{\sqrt{29}}
\end{align*}
$\sankaku{ABC}$ の面積が10のとき,$d=h=\dfrac{20}{\sqrt{29}}$ であるからd&=\dfrac{\abs{5t-2\Cdot2t-11}}{\sqrt{5^2+(-2)^2}} \\[4pt]
&=\dfrac{\abs{t-11}}{\sqrt{29}}
\end{align*}
\begin{align*}
&\dfrac{\abs{t-11}}{\sqrt{29}}=\dfrac{20}{\sqrt{29}} \\[4pt]
&\abs{t-11}=20 \\[4pt]
&t-11=\pm20 \\[4pt]
&t=-9,~31
\end{align*}
したがって,求める点Aの座標は $(-9,~-18)$,$(31,~62)$&\dfrac{\abs{t-11}}{\sqrt{29}}=\dfrac{20}{\sqrt{29}} \\[4pt]
&\abs{t-11}=20 \\[4pt]
&t-11=\pm20 \\[4pt]
&t=-9,~31
\end{align*}

ヒロ
$\myBox{ア}$ と $\myBox{イ}$ に大小関係が与えられていることに注意しよう。


















