Contents
三角形の面積と点と直線の距離

ヒロ
平面上の3点を頂点とする三角形の面積を考える。
【三角形の面積】
平面上の3点を頂点とする三角形の面積を考えるが,3点のうち1点を通るように座標軸を定めることができるため,原点を1つの頂点とする三角形の面積を考える。
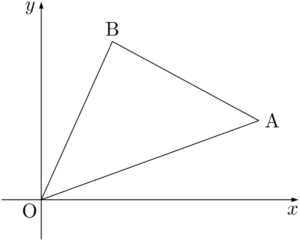
三角形の辺が座標軸と平行になっているときは,座標軸と平行な辺を底辺と見るのが基本である。例えば,点Aが $x$ 軸上にあったり,点Bが $y$ 軸上にある場合は,底辺と高さを簡単に求めることができるため,面積も簡単に求めることができる。三角形のどの辺も座標軸と平行でない場合は,上図のようになっている。辺OAの長さを $a$ として,点Bから直線OAに下ろした垂線の長さを $h$ とすると,三角形OABの面積 $S$ は
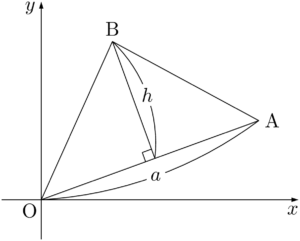
平面上の3点を頂点とする三角形の面積を考えるが,3点のうち1点を通るように座標軸を定めることができるため,原点を1つの頂点とする三角形の面積を考える。

三角形の辺が座標軸と平行になっているときは,座標軸と平行な辺を底辺と見るのが基本である。例えば,点Aが $x$ 軸上にあったり,点Bが $y$ 軸上にある場合は,底辺と高さを簡単に求めることができるため,面積も簡単に求めることができる。三角形のどの辺も座標軸と平行でない場合は,上図のようになっている。辺OAの長さを $a$ として,点Bから直線OAに下ろした垂線の長さを $h$ とすると,三角形OABの面積 $S$ は
\begin{align*}
S=\dfrac{1}{2}ah
\end{align*}
と表せる。ここで,OAの長さについては,2点間の距離の公式を用いて求めることができる。また,$h$ は点と直線の距離の公式を用いて求めることができる。S=\dfrac{1}{2}ah
\end{align*}

三角形の面積を求めよう

ヒロ
それでは具体的に三角形の面積を求める練習をしてみよう。
三角形の面積を求める問題平面上の2点A$(7,~2)$,B$(3,~6)$ と原点を頂点とする三角形OABの面積 $S$ を求めよ。
点と直線の距離を利用する
【考え方と解答】
三角形OABを図示すると次のようになる。
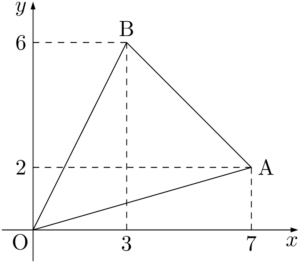
OAを底辺とみて,OAの長さを求める。
直線OAの方程式は $2x-7y=0$ であるから
三角形OABを図示すると次のようになる。

OAを底辺とみて,OAの長さを求める。
\begin{align*}
\text{OA}=\sqrt{7^2+2^2}=\sqrt{53}
\end{align*}
点Bと直線OAとの距離が高さ $h$ になる。\text{OA}=\sqrt{7^2+2^2}=\sqrt{53}
\end{align*}
直線OAの方程式は $2x-7y=0$ であるから
\begin{align*}
h=\dfrac{\abs{2\Cdot3-7\Cdot6}}{\sqrt{2^2+(-7)^2}}=\dfrac{36}{\sqrt{53}}
\end{align*}
よって,h=\dfrac{\abs{2\Cdot3-7\Cdot6}}{\sqrt{2^2+(-7)^2}}=\dfrac{36}{\sqrt{53}}
\end{align*}
\begin{align*}
S&=\dfrac{1}{2}\Cdota\text{OA}\Cdota h \\[4pt]
&=\dfrac{1}{2}\Cdota\sqrt{53}\Cdota\dfrac{36}{\sqrt{53}} \\[4pt]
&=18
\end{align*}
S&=\dfrac{1}{2}\Cdota\text{OA}\Cdota h \\[4pt]
&=\dfrac{1}{2}\Cdota\sqrt{53}\Cdota\dfrac{36}{\sqrt{53}} \\[4pt]
&=18
\end{align*}
長方形と三角形の組合せを考える

ヒロ
点と直線の距離の公式を知らない場合は,長方形と三角形の組み合わせを考えて三角形の面積を求めるだろう。
平面上の2点A$(7,~2)$,B$(3,~6)$ と原点を頂点とする三角形OABの面積 $S$ を求めよ。
【考え方と解答】
3点O,A,Bを通り,座標軸と平行な辺で作られる長方形OPQRを考える。
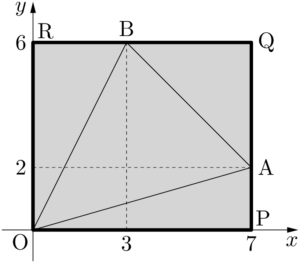
この長方形の面積を $T$ とすると
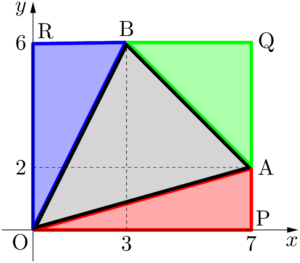
$\sankaku{OAP}$,$\sankaku{ABQ}$,$\sankaku{OBR}$ の面積をそれぞれ $S_1,~S_2,~S_3$ とすると
3点O,A,Bを通り,座標軸と平行な辺で作られる長方形OPQRを考える。

この長方形の面積を $T$ とすると
\begin{align*}
T=7\times6=42
\end{align*}
であり,この長方形の面積から3つの三角形 $\sankaku{OAP}$,$\sankaku{ABQ}$,$\sankaku{OBR}$ の面積を引くことで $\sankaku{OAB}$ の面積を求めることができる。T=7\times6=42
\end{align*}

$\sankaku{OAP}$,$\sankaku{ABQ}$,$\sankaku{OBR}$ の面積をそれぞれ $S_1,~S_2,~S_3$ とすると
\begin{align*}
&\textcolor{red}{S_1}=\dfrac{1}{2}\Cdota7\Cdota2=7 \\[4pt]
&\textcolor{green}{S_2}=\dfrac{1}{2}\Cdota(7-3)\Cdota(6-2)=8 \\[4pt]
&\textcolor{blue}{S_3}=\dfrac{1}{2}\Cdota6\Cdota3=9
\end{align*}
したがって&\textcolor{red}{S_1}=\dfrac{1}{2}\Cdota7\Cdota2=7 \\[4pt]
&\textcolor{green}{S_2}=\dfrac{1}{2}\Cdota(7-3)\Cdota(6-2)=8 \\[4pt]
&\textcolor{blue}{S_3}=\dfrac{1}{2}\Cdota6\Cdota3=9
\end{align*}
\begin{align*}
S&=T-(S_1+S_2+S_3) \\[4pt]
&=42-(7+8+9) \\[4pt]
&=18
\end{align*}
S&=T-(S_1+S_2+S_3) \\[4pt]
&=42-(7+8+9) \\[4pt]
&=18
\end{align*}
長方形と三角形の組合せを考える part2

ヒロ
上の方法では,長方形と三角形の組み合わせを考えて「引き算」で三角形OABの面積を求めたが,「足し算」で求める方法を考える人もいるだろう。
平面上の2点A$(7,~2)$,B$(3,~6)$ と原点を頂点とする三角形OABの面積 $S$ を求めよ。
【考え方と解答】
上で考えた3点P,Q,R以外に,さらに3点C$(3,~2)$,D$(3,~0)$,E$(0,~2)$ を考える。三角形OABを3つの三角形 $\sankaku{OAC},~\sankaku{OBC},~\sankaku{ABC}$ に分割する。
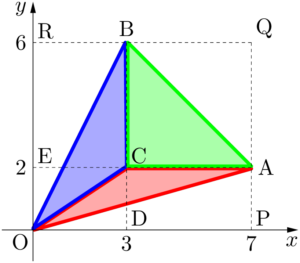
ここで,赤と青の2つの三角形 $\sankaku{OAC}$,$\sankaku{OBC}$ について,等積変形を行うと次のように,$\sankaku{OAC}$ を $\sankaku{ACD}$ に,$\sankaku{OBC}$ を $\sankaku{BCE}$ に移すことができる。
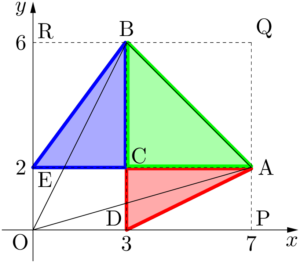
この等積変形によって,三角形OABの面積(赤・青・緑の3つの三角形の面積の和)は次の図の灰色部分の面積の半分に等しいことが分かる。
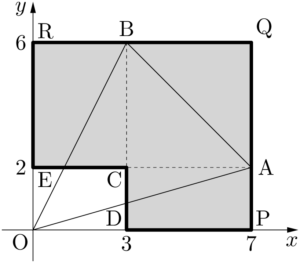
三つの長方形RECB,CDPA,AQBCの面積の和を計算しても良いが,多くの人は長方形OPQRの面積から長方形ODCEの面積を引いて計算するだろう。
したがって,三角形OABの面積 $S$ は
上で考えた3点P,Q,R以外に,さらに3点C$(3,~2)$,D$(3,~0)$,E$(0,~2)$ を考える。三角形OABを3つの三角形 $\sankaku{OAC},~\sankaku{OBC},~\sankaku{ABC}$ に分割する。

ここで,赤と青の2つの三角形 $\sankaku{OAC}$,$\sankaku{OBC}$ について,等積変形を行うと次のように,$\sankaku{OAC}$ を $\sankaku{ACD}$ に,$\sankaku{OBC}$ を $\sankaku{BCE}$ に移すことができる。

この等積変形によって,三角形OABの面積(赤・青・緑の3つの三角形の面積の和)は次の図の灰色部分の面積の半分に等しいことが分かる。

三つの長方形RECB,CDPA,AQBCの面積の和を計算しても良いが,多くの人は長方形OPQRの面積から長方形ODCEの面積を引いて計算するだろう。
したがって,三角形OABの面積 $S$ は
\begin{align*}
S&=\dfrac{1}{2}(7\Cdota6-3\Cdota2)=18
\end{align*}
S&=\dfrac{1}{2}(7\Cdota6-3\Cdota2)=18
\end{align*}


















