Contents
円外の点から円に引いた接線【京都産業大】
2016年 京都産業大座標平面において,原点を中心とし半径が1の円に点$(0,~2)$ を通る直線 $l$ が接するとき,$l$ の傾きは $\myhako$ である。
【考え方と解答】
原点を中心とし半径が1の円を $C$ とする。点$(0,~2)$ を通り $x$ 軸に垂直な直線は $C$ の接線にならないから,求める接線は
原点を中心とし半径が1の円を $C$ とする。点$(0,~2)$ を通り $x$ 軸に垂直な直線は $C$ の接線にならないから,求める接線は
\begin{align*}
&y=mx+2 \\[4pt]
&mx-y+2=0
\end{align*}
と表せる。この直線と原点との距離が半径1と等しいから&y=mx+2 \\[4pt]
&mx-y+2=0
\end{align*}
\begin{align*}
&\dfrac{\abs{m\cdot0-0+2}}{\sqrt{m^2+1}}=1 \\[4pt]
&2=\sqrt{m^2+1}
\end{align*}
両辺2乗すると&\dfrac{\abs{m\cdot0-0+2}}{\sqrt{m^2+1}}=1 \\[4pt]
&2=\sqrt{m^2+1}
\end{align*}
\begin{align*}
&m^2+1=4 \\[4pt]
&m^2=3 \\[4pt]
&m=\pm\sqrt{3}
\end{align*}
よって,求める接線 $l$ の傾きは $\pm\sqrt{3}$&m^2+1=4 \\[4pt]
&m^2=3 \\[4pt]
&m=\pm\sqrt{3}
\end{align*}

ヒロ
図を描いて考える人や,図を想像した人にとっては,簡単な問題だったかもしれない。

ヒロ
面倒な計算をすることなく,接線の傾きを求めてしまったかもしれない。別解として書いておく。
【別の考え方と解答】
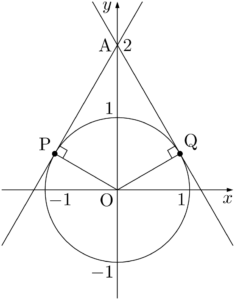
点$(0,~2)$ を点Aとし,接点を下図のように点P,Qとする。
$\sankaku{OAP}$ に着目すると
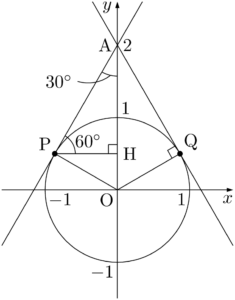
分かりやすくするために,点Pから $y$ 軸へ垂線PHを下ろすと,$\kaku{APH}=60\Deg$ となる。
直線APの傾きは $\dfrac{\text{AH}}{\text{PH}}$ であり,これは三角比を用いると
点$(0,~2)$ を点Aとし,接点を下図のように点P,Qとする。

$\sankaku{OAP}$ に着目すると
\begin{align*}
\text{OA}=2,~\text{OP}=1,~\kaku{OPA}=90\Deg
\end{align*}
であるから,$\kaku{OAP}=30\Deg$ と分かる。\text{OA}=2,~\text{OP}=1,~\kaku{OPA}=90\Deg
\end{align*}
分かりやすくするために,点Pから $y$ 軸へ垂線PHを下ろすと,$\kaku{APH}=60\Deg$ となる。

直線APの傾きは $\dfrac{\text{AH}}{\text{PH}}$ であり,これは三角比を用いると
\begin{align*}
\dfrac{\text{AH}}{\text{PH}}&=\tan\kaku{APH} \\[4pt]
&=\tan60\Deg=\sqrt{3}
\end{align*}
$y$ 軸に関して対称だから,直線AQの傾きは $-\sqrt{3}$ となる。\dfrac{\text{AH}}{\text{PH}}&=\tan\kaku{APH} \\[4pt]
&=\tan60\Deg=\sqrt{3}
\end{align*}
円外の点から円に引いた接線の本数【東京理科大】
2020年 東京理科大座標平面上に,方程式 $x^2+y^2=4$ の表す円 $C$ と,点P$(-4,~2)$ がある。Pを通る $C$ の2本の接線の方程式をそれぞれ求めよ。
【考え方と解答】
Pを通る $C$ の接線は $y$ 軸と平行でないから,求める接線の方程式は
Pを通る $C$ の接線は $y$ 軸と平行でないから,求める接線の方程式は
\begin{align*}
&y=m(x+4)+2 \\[4pt]
&mx-y+4m+2=0
\end{align*}
と表せる。この直線が $C$ と接するのは,原点との距離が2のときだから&y=m(x+4)+2 \\[4pt]
&mx-y+4m+2=0
\end{align*}
\begin{align*}
&\dfrac{\abs{4m+2}}{\sqrt{m^2+1}}=2 \\[4pt]
&\abs{2m+1}=\sqrt{m^2+1}
\end{align*}
両辺を2乗して&\dfrac{\abs{4m+2}}{\sqrt{m^2+1}}=2 \\[4pt]
&\abs{2m+1}=\sqrt{m^2+1}
\end{align*}
\begin{align*}
&(2m+1)^2=m^2+1 \\[4pt]
&3m^2+4m=0 \\[4pt]
&m(3m+4)=0 \\[4pt]
&m=0,~-\dfrac{4}{3}
\end{align*}
よって,求める2本の接線の方程式は&(2m+1)^2=m^2+1 \\[4pt]
&3m^2+4m=0 \\[4pt]
&m(3m+4)=0 \\[4pt]
&m=0,~-\dfrac{4}{3}
\end{align*}
\begin{align*}
y=2,~y=-\dfrac{4}{3}x-\dfrac{10}{3}
\end{align*}
y=2,~y=-\dfrac{4}{3}x-\dfrac{10}{3}
\end{align*}


















