Contents
1次式で割る組立除法

ヒロ
では,組立除法のやり方を説明していくよ。

ヒロ
まずは割られる整式 $5x^3+6x+8$ の係数を次数が高い方から順に書いていく。今回の場合,5,0,6,8 を左から順に書こう。割られる整式には $x^2$ の項がないけど,係数が0で $0x^2$ として,ちゃんと0を書くようにしよう。

ヒロ
次に,左側に割る式 $x+1$ が0になる $x$ の値 $-1$ を書こう。そして1行空けて横線を引こう。
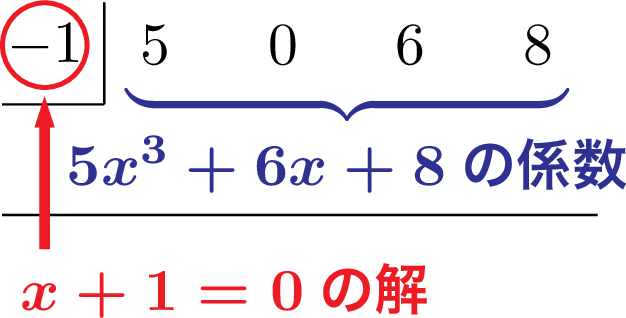

ヒロ
これで組立除法の準備ができたことになる。

ここまでは大丈夫です。

ヒロ
まず,一番目の係数5をそのまま下ろそう。


ヒロ
次に,今下ろした係数 5 と左上の $-1$ を掛けて,$-5$ を2番目の係数 0 の下に書こう。


ヒロ
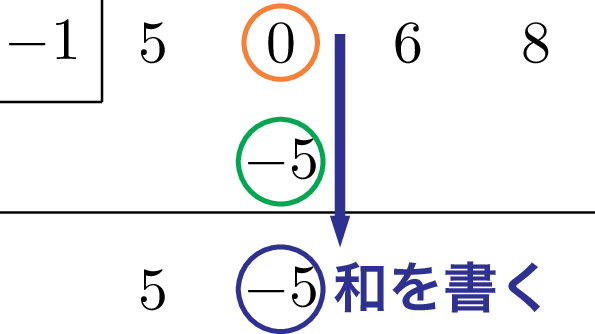
縦に並んだ2数 0 と $-5$ の和 $-5$ を横線の下に書こう。

ヒロ
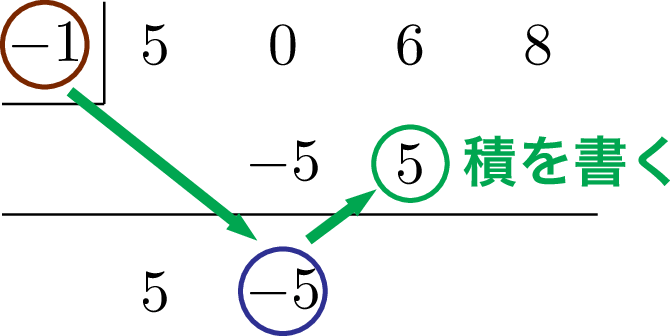
横線の下に書いた数 $-5$ と左上の $-1$ の積,つまり 5 を3番目の係数 6 の下に書こう。

ヒロ
縦に並んだ2数 6 と 5 の和 11 を横線の下に書こう。
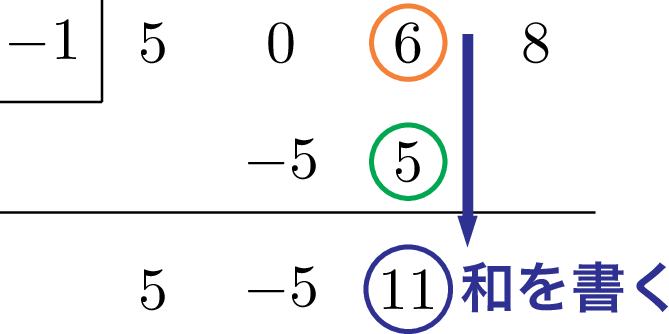

ヒロ
そろそろ要領は分かってきたかな?横線の下に書いた数と左上の数の積 $-1\times11$ つまり $-11$ を最後の係数 8 の下に書こう。
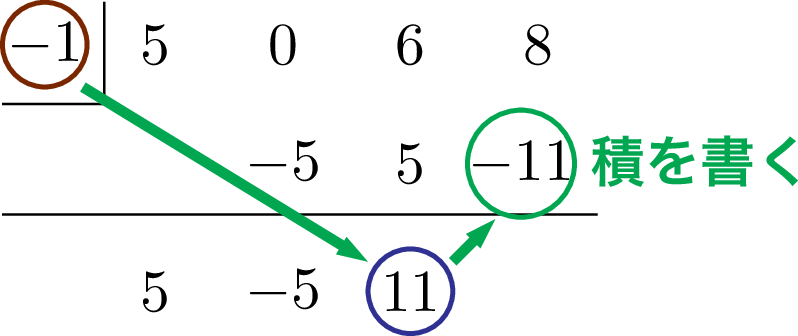

ヒロ
縦に並んだ2数 8 と $-11$ の和 $-3$ を横線の下に書こう。
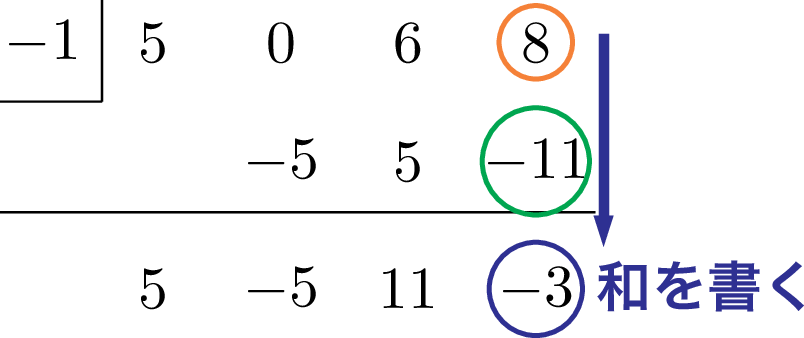

ヒロ
1つずつゆっくりやったけど,サクサク書けるようにしよう!まず,下ろす。次に掛けて,足す。これを繰り返すだけだ。
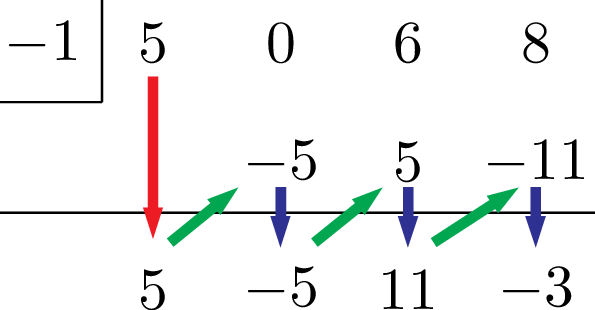

分かりました!

ヒロ
4つの数が得られたわけだけど,今は1次式で割っているから余りは定数になるから,一番右側の$-3$が余りになって,左3つの数が商を表してるよ。3次式を1次式で割っているから,商は2次式になるね。


つまり,商は $5x^2-5x+11$,余りは $-3$ ってことですね!