2016年センター試験 数学ⅠA 第2問 三角比

2016年センター試験数学ⅠA 第2問三角比の解説をします。

まだ問題を解いていない人は解いてから解説を読んでください。

2016年センターⅠA 第2問三角比　$\sankaku{ABC}$ の辺の長さと角の大きさを測ったところ，$\mathrm{AB}=7\sqrt{3}$ および $\kaku{ACB}=60\Deg$ であった。したがって，$\sankaku{ABC}$ の外接円Oの半径は $\myBox{ア}$ である。
　外接円Oの，点Cを含む弧AB上で点Pを動かす。
(1) $2\mathrm{PA}=3\mathrm{PB}$ となるのは $\mathrm{PA}=\myBox{イ}\sqrt{\myBox{ウエ}}$ のときである。
(2) $\sankaku{PAB}$ の面積が最大となるのは $\mathrm{PA}=\myBox{オ}\sqrt{\myBox{カ}}$ のときである。
(3) $\sin\kaku{PBA}$ の値が最大となるのは $\mathrm{PA}=\myBox{キク}$ のときであり，このとき $\sankaku{PAB}$ の面積は $\dfrac{\myBox{ケコ}\sqrt{\myBox{サ}}}{\myBox{シ}}$ である。

Contents

1 ウォーミングアップ問題の解答
2 (1)の解答
3 (2)の解答
4 (3)の解答
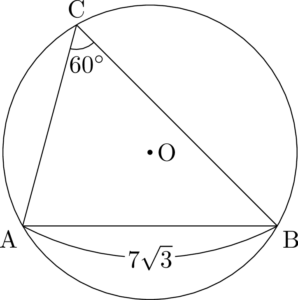
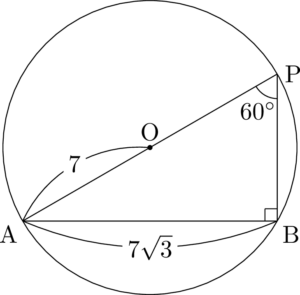
5 2016年センター数学ⅠA 三角比を解いた感想

ウォーミングアップ問題の解答

ヒロ

小問に入る前の問題ということで，最も基本的な外接円の半径を求める問題だね。

【アの解答】
$\sankaku{ABC}$ の外接円の半径を $R$ とすると，正弦定理より

\begin{align*}
R&=\dfrac{\mathrm{AB}}{2\sin\kaku{ACB}} \\[4pt]
&=\dfrac{7\sqrt{3}}{2\Cdota\dfrac{\sqrt{3}}{2}} \\[4pt]
&=7
\end{align*}

(1)の解答

ヒロ

まずは状況を把握するために図を描いてみよう。

【状況を把握するための図】
外接円が絡む図では，円から描くと綺麗に描くことができる。また，三角形の内角の1つが $60\Deg$ だから，円さえ綺麗に描ければかなり正確な図を描くことができる。

ヒロ

円に内接する三角形の内角の1つが $60\Deg$ のときに正確な図を描く方法については，次の記事を参考にして欲しい。

2006年センター試験数学IA 図形【円に内接する正三角形・方べきの定理】

2006年センター数学IA図形の問題を解説します。方べきの定理をどのように使うかを知っておくことで，スムーズに問題を解くことができます。また，円に内接する正三角形の描き方を知っておくと，速く綺麗に描くことができます。

ヒロ

いまは外接円Oの点Cを含む弧AB上で点Pを動かすから，$\kaku{APB}=60\Deg$ であることが分かる。

ヒロ

また，$2\mathrm{PA}=3\mathrm{PB}$ より，$\mathrm{PA}:\mathrm{PB}=3:2$ となるから次の図のようになる。

【(1)の$\sankaku{PAB}$ を表した図】

ヒロ

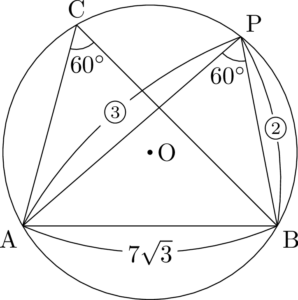
PAとPBの比が分かっているから，PAとPBの長さを1つの文字を使って表せるから，通常は余弦定理で処理するだろう。

ヒロ

ただ，このブログの読者であれば，2と3と $60\Deg$ を見て反応するかもしれない。これって「ルナ三角形だろ！」と。

ヒロ

「ルナ三角形って何？」ってなる人は，次の記事で知識を補っておこう。

1999年センター試験数学IA 図形【ルナ三角形と那覇三角形】

1998年センターIAの図形の問題を解説しています。「ルナ三角形」や「那覇三角形」を知っていると，時短になるので覚えておこう。また，正弦定理は垂線の長さに着目することで分数になることを避けることができる。

【イ～エの解答】
$\sankaku{PAB}$ は3辺の長さの比が $2:3:\sqrt{7}$ のルナ三角形の1つであることが分かる。比の $\sqrt{7}$ に相当するABの長さが $\mathrm{AB}=7\sqrt{3}$ であるから，比から辺の長さに変換するには $\sqrt{21}$ を掛ければよいことが分かる。よって，

\begin{align*}
\mathrm{PA}=3\sqrt{21}
\end{align*}

ヒロ

真面目に余弦定理で求めると，次のようになる。

【イ～エの別解】
$2\mathrm{PA}=3\mathrm{PB}$ より，正の数 $x$ を用いて

\begin{align*}
\mathrm{PA}=3x,~\mathrm{PB}=2x
\end{align*}

と表せる。$\sankaku{PAB}$ において余弦定理より

\begin{align*}
&\mathrm{PA}^2+\mathrm{PB}^2-2\mathrm{PA}\Cdota\mathrm{PB}\cos\kaku{APB}=\mathrm{AB}^2 \\[4pt]
&9x^2+4x^2-2\Cdota3x\Cdota2x\Cdota\dfrac{1}{2}=(7\sqrt{3})^2 \\[4pt]
&7x^2=49\Cdota3 \\[4pt]
&x^2=21
\end{align*}

$x>0$ より，$x=\sqrt{21}$
よって，$\mathrm{PA}=3\sqrt{21}$

ヒロ

ルナ三角形を使える知識になっている人にとっては，とても面倒な計算になる。

【マーク式試験における裏技の是非】
こういう浅い知識で解くのは良くないと目くじらを立てる人もいるが，そういう人は次のような直角三角形の一辺の長さ $x$ を求める問題でも，わざわざ三平方の定理を使って辺の長さを求めるのだろうか？

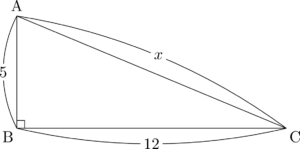
「これは $5:12:13$ の有名直角三角形だから，即座に $x=13$ として良い」と反論するのなら，ルナ三角形だって同じである。
　そもそも有名かどうかなんて人によって違うのである。ルナ三角形という名前は置いといて，辺の長さの比が $2:3:\sqrt{7}$ で，$\sqrt{7}$ の対角が $60\Deg$ である三角形を，有名三角形として覚えている人なんていっぱいいるだろう。
　あとは，こういうのを許さないというのなら，すべての数学の試験を記述式にしてしまえば良いのである。マーク式試験では，知識がある者が有利になるのは当然の結果である。しかし，使えるレベルの知識になるには，それ相応の努力が必要なのは言うまでもない。それが簡単な $5:12:13$ の直角三角形であったとしても，知らない人からすれば「計算せずに求められるのはずるい」となってしまう。
　知識が簡単かどうかは人によって異なるため，使える知識になるならどんどん使えば良いと思う。

(2)の解答

(2) $\sankaku{PAB}$ の面積が最大となるのは $\mathrm{PA}=\myBox{オ}\sqrt{\myBox{カ}}$ のときである。

ヒロ

次は三角形の面積が最大になるときのPAの長さを求める問題。

【オカの解答】
点Pが弧AB上を動いて，$\sankaku{PAB}$ の面積が最大になるのは，点Pと辺ABの距離が最大になるときである。つまり，円の中心を通り，辺ABと垂直な直線と円の交点をPとすればよい。

このとき，$\mathrm{PA}=\mathrm{PB}$ となるから，$\sankaku{PAB}$ は正三角形になる。よって，$\mathrm{PA}=7\sqrt{3}$ である。

(3)の解答

(3) $\sin\kaku{PBA}$ の値が最大となるのは $\mathrm{PA}=\myBox{キク}$ のときであり，このとき $\sankaku{PAB}$ の面積は $\dfrac{\myBox{ケコ}\sqrt{\myBox{サ}}}{\myBox{シ}}$ である。

ヒロ

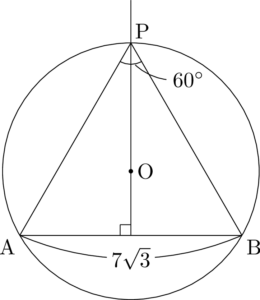
次は $\sin$ の値が最大になるときのPAの長さを求める問題。

【キクの解答】
　一般に，$0\Deg\leqq\theta\leqq180\Deg$ のとき，$0\leqq\sin\theta\leqq1$ であるから，$\kaku{PBA}=90\Deg$ となることがあるのなら，そのときのPAの長さを求めれば良いことになる。
　実際，次の図のように，APが直径となるように点Pをとれば，$\kaku{PBA}=90\Deg$ になる。

このとき，$\mathrm{PA}=2R=14$ である。

ヒロ

最後の三角形の面積はボーナス問題。

【ケ～シの解答】
$\sankaku{PAB}$ は $1:2:\sqrt{3}$ の有名直角三角形であるから，$\mathrm{PB}=7$ である。よって，

\begin{align*}
\sankaku{PAB}&=\dfrac{1}{2}\Cdota\mathrm{AB}\Cdota\mathrm{PB} \\[4pt]
&=\dfrac{1}{2}\Cdota7\sqrt{3}\Cdota7 \\[4pt]
&=\dfrac{49\sqrt{3}}{2}
\end{align*}