Contents
$x$ の係数が1でない1次式で割る

ヒロ
じゃあ次の問題をやってみよう。
問題$2x^3-5x^2-5$ を $2x-1$ で割ったときの商と余りを求めよ。
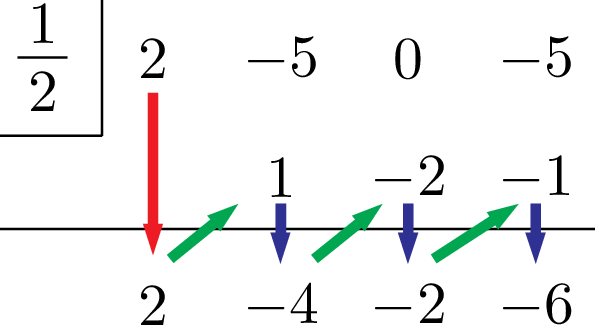

組立除法終わりました!

ヒロ
じゃあ商と余りは?

商は $2x^2-4x-2$ で,余りは $-6$ ですね。

ヒロ
余りは合ってるけど,商は違うよ?

言われた通りにやって,違うってどういうことですか・・・

ヒロ
ある程度意味を考えないとね?

はい・・・

ヒロ
その計算は $2x-1$ ではなくて,$\displaystyle x-\frac{1}{2}$ で割ってることになるんだよ。
\begin{align*}
2x^3-5x^2-5=\left(x-\frac{1}{2}\right)(2x^2-4x-2)-6
\end{align*}
2x^3-5x^2-5=\left(x-\frac{1}{2}\right)(2x^2-4x-2)-6
\end{align*}

確かにそうですね。右辺を展開すれば左辺になります。

ヒロ
だからこの式を変形すれば・・・
\begin{align*}
2x^3-5x^2-5&=\left(x-\frac{1}{2}\right)(2x^2-4x-2)-6 \\[4pt]
&=\left(x-\frac{1}{2}\right)\cdot2(x^2-2x-1)-6 \\[4pt]
&=(2x-1)(x^2-2x-1)-6
\end{align*}
2x^3-5x^2-5&=\left(x-\frac{1}{2}\right)(2x^2-4x-2)-6 \\[4pt]
&=\left(x-\frac{1}{2}\right)\cdot2(x^2-2x-1)-6 \\[4pt]
&=(2x-1)(x^2-2x-1)-6
\end{align*}

ヒロ
これで商は $x^2-2x-1$ だと分かるでしょ?

そうですね。

ヒロ
ということで,これを組立除法に組み込むとこうなるよ。


なるほど!商の部分だけ $x$ の係数で割れば良いんですね。


ヒロ
ということで,商は $x^2-2x-1$,余りは $-6$ だね。

ヒロ
次は2次式で割る組立除法,いわゆる「スーパー組立除法」について説明していく。