Contents
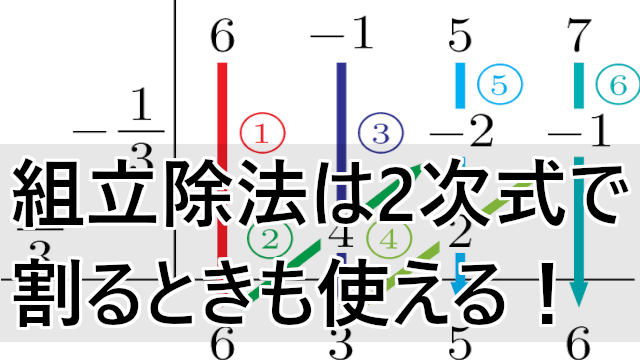
2次式で割る組立除法 (スーパー組立除法)

ではこの調子で次の問題をやってみよう!

2次式で割るとか卑怯ですよ。筆算じゃないとできないじゃないですか!

え?組立除法でできるでしょ?

組立除法は1次式で割るときしか使えないって習いましたよ?

確かに教科書には1次式で割るときしか使えないように載ってるね。

でもよく考えて欲しい。そんなピンポイントでしか使えないものをわざわざ考えると思う?組立除法ってかなり効率の良い記述法だよね。それを高次式の除法に応用しようと考えるのが当然だと思うんだ。

言いたいことは分かりますけど,そんな変人,まわりにいません。

誰が変人だ・・・

さて・・・2次式で割る組立除法を説明していこう。

名付けてスーパー組立除法!

・・・・

まずは割られる整式 $2x^3-3x^2+4$ の係数を次数が高い方から順に書いていく。今回の場合,2,$-3$,0,4 を左から順に書こう。割られる整式には $x$ の項がないが,係数が0で $0x$ として,ちゃんと0を書くようにしよう。

次に,左に割る式 $x^2-3x+2$ の定数項を符号を変えて書こう。その左下に $x$ の係数を符号を変えて書こう。書きやすさを考えて左にずらしたけど,別にずらさなくてもできる人はずらさなくて良いからね。

縦線と横線を引いて,スーパー組立除法の準備ができたことになる。


ちょっとややこしいけど慣れるしかないですね。

1次式で割るときと同様,最初の係数をそのまま下ろそう。
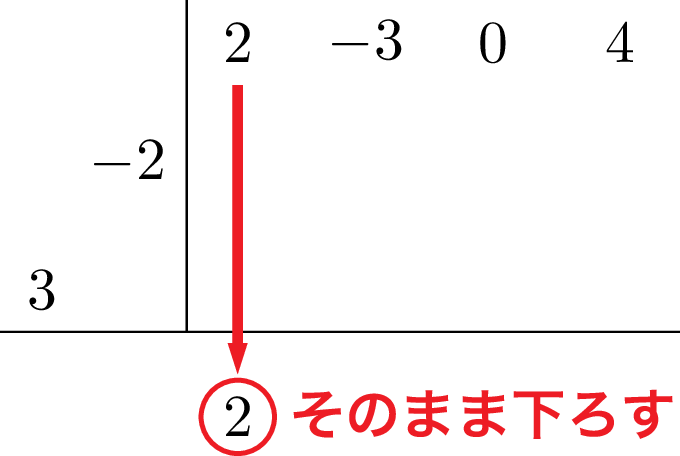

次に,今書いた 2 と縦線の左側の数字を掛けて,書く位置に注意して右上に書こう。
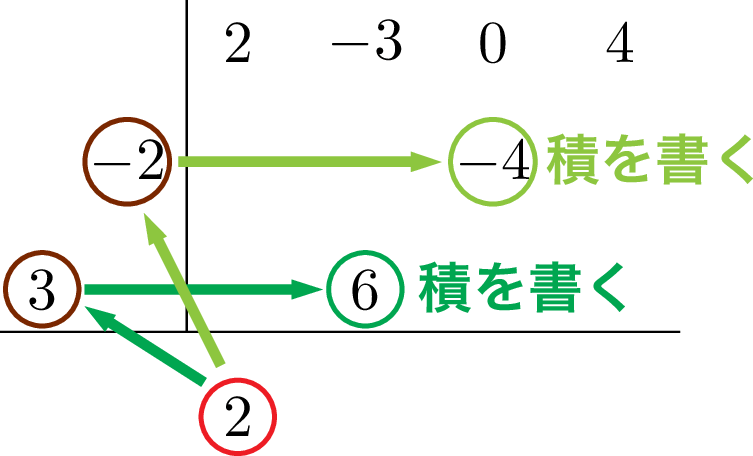

次に縦に並んだ数の和を横線の下に書こう。
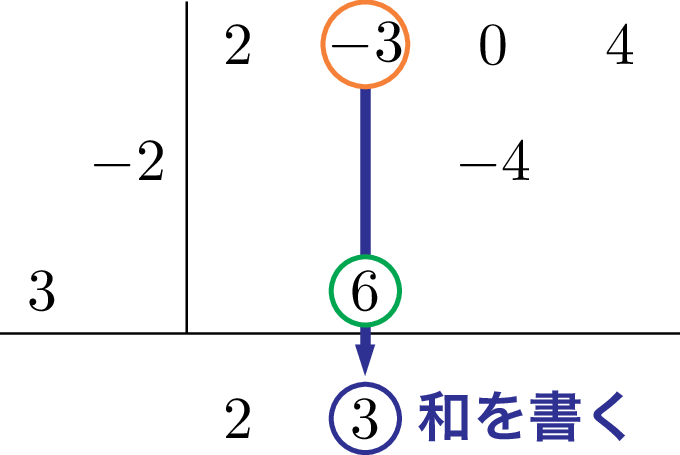

今書いた 3 と縦線の左側の数字を掛けて,書く位置に注意して右上に書こう。
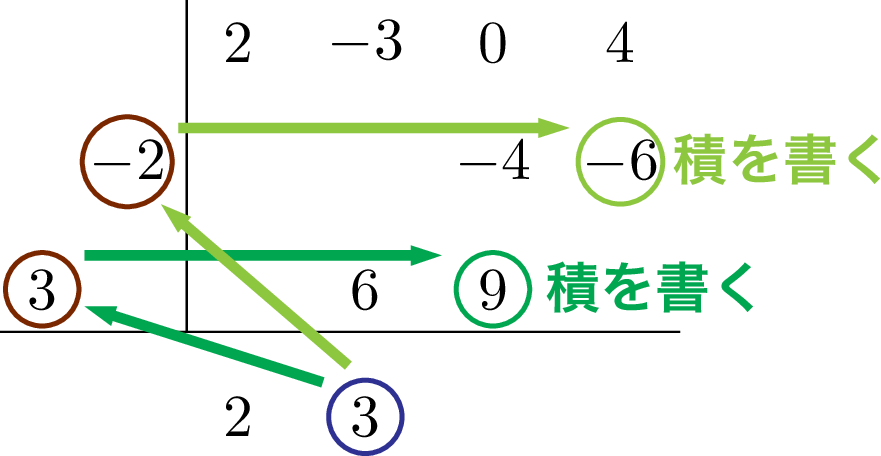

さっきと同じように縦に並んだ数の和を横線の下に書こう。
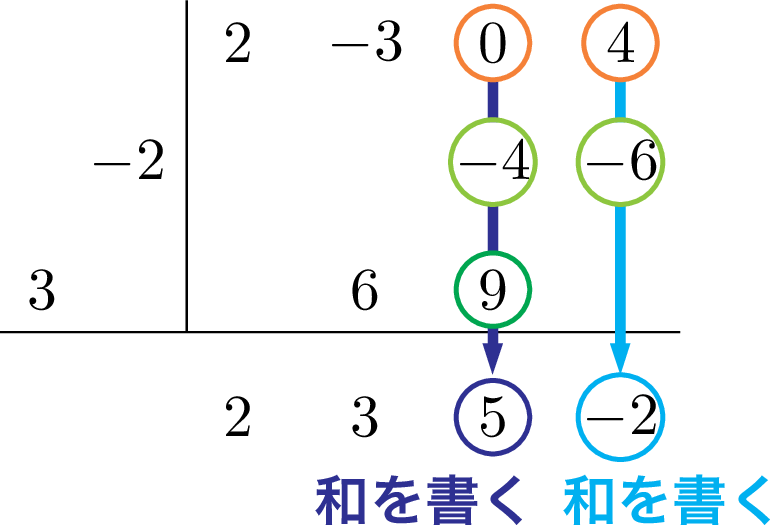

一番右側の定数項の下が埋まっているので,これも縦に並んだ数の和を横線の下に書こう。

割る式の係数をずらして書いたのは,積を書くときにどこに書けば良いかを分かりやすくするためで,丸で囲んだ数字の順番に埋めていけば良いよ。
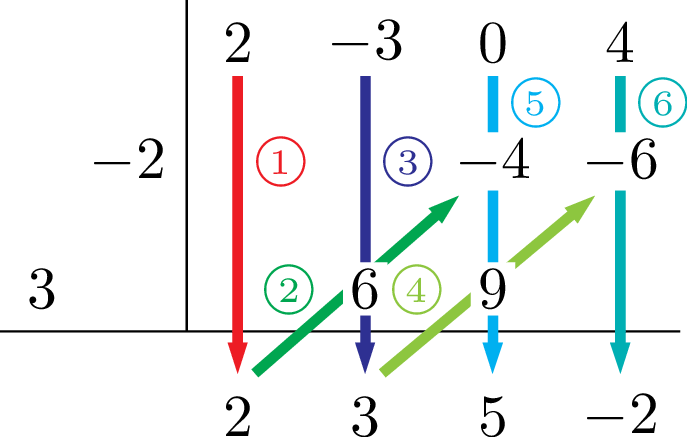

分かりました!

今回は2次式で割っているので,余りは1次式または定数になるから,右2つが余りになるよ。残りの2つが商で,3次式を2次式で割っているから商は1次式ということを考えると,左の数字が $x$ の係数で,右の数字が定数項になるね。


つまり,商は $2x+3$,余りは $5x-2$ だね。