2019年 センター試験 数学ⅡB 第4問 ベクトル

2019年のセンター試験数学ⅡB 第4問ベクトルの解説をします。

まだ問題を解いていない人は解いてから解説を読んでください。

2019年センターⅡB ベクトル四角形ABCDを底面とする四角錐OABCDを考える。四角形ABCDは，辺ADと辺BCが平行で，$\mathrm{AB=CD}$, $\kaku{ABC}=\kaku{BCD}$ を満たすとする。さらに，$\Vec{OA}=\vec{a}$, $\Vec{OB}=\vec{b}$, $\Vec{OC}=\vec{c}$ として

\begin{align*}
&\abs{\vec{a}}=1,~\abs{\vec{b}}=\sqrt{3},~\abs{\vec{c}}=\sqrt{5} \\[4pt]
&\vec{a}\Cdota\vec{b}=1,~\vec{b}\Cdota\vec{c}=3,~\vec{a}\Cdota\vec{c}=0
\end{align*}

であるとする。
(1) $\kaku{AOC}=\myBox{アイ}\Deg$ により，三角形OACの面積は $\dfrac{\sqrt{\myBox{ウ}}}{\myBox{エ}}$ である。
(2) $\Vec{BA}\Cdot\Vec{BC}=\myBox{オカ}$, $\abs{\Vec{BA}}=\sqrt{\myBox{キ}}$, $\abs{\Vec{BC}}=\sqrt{\myBox{ク}}$ であるから，$\kaku{ABC}=\myBox{ケコサ}\Deg$ である。さらに，辺ADと辺BCが平行であるから，$\kaku{BAD}=\kaku{ADC}=\myBox{シス}\Deg$ である。よって，$\Vec{AD}=\myBox{セ}~\Vec{BC}$ であり

\begin{align*}
\Vec{OD}=\vec{a}-\myBox{ソ}~\vec{b}+\myBox{タ}~\vec{c}
\end{align*}

と表される。また，四角形ABCDの面積は $\dfrac{\myBox{チ}\sqrt{\myBox{ツ}}}{\myBox{テ}}$ である。
(3) 三角形OACを底面とする三角錐BOACの体積 $V$ を求めよう。
3点O, A, Cの定める平面 $\alpha$ 上に，点Hを $\Vec{BH}\perp\vec{a}$ と $\Vec{BH}\perp\vec{c}$ が成り立つようにとる。$\abs{\Vec{BH}}$ は三角錐BOACの高さである。Hは $\alpha$ 上の点であるから，実数 $s,~t$ を用いて $\Vec{OH}=s\vec{a}+t\vec{c}$ の形に表される。
$\Vec{BH}\Cdot\vec{a}=\myBox{ト}$, $\Vec{BH}\Cdot\vec{c}=\mybox{ト}$ により，$s=\myBox{ナ}$, $t=\dfrac{\myBox{ニ}}{\myBox{ヌ}}$ である。よって，$\abs{\Vec{BH}}=\dfrac{\sqrt{\myBox{ネ}}}{\myBox{ノ}}$ が得られる。したがって，(1)により，$V=\dfrac{\myBox{ハ}}{\myBox{ヒ}}$ であることがわかる。
(4) (3)の $V$ を用いると，四角錐OABCDの体積は $\myBox{フ}~V$ と表せる。さらに，四角形ABCDを底面とする四角錐OABCDの高さは $\dfrac{\sqrt{\myBox{ヘ}}}{\myBox{ホ}}$ である。

Contents

1 センターⅡB ベクトルを解くときの図を描くタイミング
2 (1)の解答
3 (2)の解答
4 (3)の解答
5 (4)の解答
6 2019年センター数学ⅡB ベクトルを解いた感想

センターⅡB ベクトルを解くときの図を描くタイミング

ヒロ

ベクトルの問題を解いていくときには，主に次の2通りに分かれる。

ヒロ

① 最初に図を描く。② 最初は図を描かずに設問に進む。

ヒロ

個人的には，平面ベクトルでは，正弦や余弦の値が与えられている場合は，うまく図を描くことで楽に問題を解くことができる可能性があるため，最初に図を描くことが多い。

ヒロ

速さを追求するなら，図を描かずに全部解くことができるならかなり速いはず。

ヒロ

ただ，最後の方の問題は，どうなっているかを把握しないといけない場合が多く，図を描く羽目になり，ある程度時間を取られる。

ヒロ

時々見かける，頭の中でサクッと状況把握できる人が羨ましいが・・・

ヒロ

どのタイミングで図を描くかは人によって異なるが，とりあえず(1)から説明していく。

(1)の解答

ヒロ

$\kaku{AOC}$ を求める問題だから，$\vec{a},~\vec{c}$ の内積と大きさに着目しよう。このとき，内積からチェックするようにしよう。もし，内積が0であれば，その時点でなす角が $90\Deg$ と決まるからね。

【アイの解答】
$\vec{a}\Cdot\vec{c}=0$ より，$\kaku{AOC}=90\Deg$

ヒロ

これで $\sankaku{OAC}$ は直角三角形と分かったから，その面積も簡単に求めることができるね。

【ウエの解答】

\begin{align*}
\sankaku{OAC}&=\dfrac{1}{2}\mathrm{OA}\Cdota\mathrm{OC} \\[4pt]
&=\dfrac{1}{2}\Cdota1\Cdota\sqrt{5} \\[4pt]
&=\dfrac{\sqrt{5}}{2}
\end{align*}

(2)の解答

(2) $\Vec{BA}\Cdot\Vec{BC}=\myBox{オカ}$, $\abs{\Vec{BA}}=\sqrt{\myBox{キ}}$, $\abs{\Vec{BC}}=\sqrt{\myBox{ク}}$ であるから，$\kaku{ABC}=\myBox{ケコサ}\Deg$ である。さらに，辺ADと辺BCが平行であるから，$\kaku{BAD}=\kaku{ADC}=\myBox{シス}\Deg$ である。よって，$\Vec{AD}=\myBox{セ}~\Vec{BC}$ であり
\begin{align*}
\Vec{OD}=\vec{a}-\myBox{ソ}~\vec{b}+\myBox{タ}~\vec{c}
\end{align*}
と表される。また，四角形ABCDの面積は $\dfrac{\myBox{チ}\sqrt{\myBox{ツ}}}{\myBox{テ}}$ である。

ヒロ

始点がBになっているので，始点をOに変えて計算していこう。

【オ～クの解答】

\begin{align*}
\Vec{BA}\Cdota\Vec{BC}&=(\vec{a}-\vec{b})\Cdota(\vec{c}-\vec{b}) \\[4pt]
&=\vec{a}\Cdota\vec{c}-\vec{a}\Cdota\vec{b}-\vec{b}\Cdota\vec{c}+\abs{\vec{b}}^2 \\[4pt]
&=0-1-3+(\sqrt{3})^2 \\[4pt]
&=-1
\end{align*}

\begin{align*}
\abs{\Vec{BA}}^2&=\abs{\vec{a}-\vec{b}}^2 \\[4pt]
&=\abs{\vec{a}}^2-2\vec{a}\Cdota\vec{b}+\abs{\vec{b}}^2 \\[4pt]
&=1^2-2\Cdota1+(\sqrt{3})^2 \\[4pt]
&=2
\end{align*}

よって，$\abs{\Vec{BA}}=\sqrt{2}$

\begin{align*}
\abs{\Vec{BC}}^2&=\abs{\vec{c}-\vec{b}}^2 \\[4pt]
&=\abs{\vec{c}}^2-2\vec{c}\Cdota\vec{b}+\abs{\vec{b}}^2 \\[4pt]
&=(\sqrt{5})^2-2\Cdota3+(\sqrt{3})^2 \\[4pt]
&=2
\end{align*}

よって，$\abs{\Vec{BC}}=\sqrt{2}$

ヒロ

次は $\kaku{ABC}$ を求める問題だから，$\Vec{BA}$ と $\Vec{BC}$ に着目して求めよう。必要な値を直前に求めているから気付くだろう。

【ケコサの解答】

\begin{align*}
\cos\kaku{ABC}&=\dfrac{\Vec{BA}\Cdot\Vec{BC}}{\abs{\Vec{BA}}\abs{\Vec{BC}}} \\[4pt]
&=\dfrac{-1}{\sqrt{2}\Cdot\sqrt{2}} \\[4pt]
&=-\dfrac{1}{2}
\end{align*}

よって，$\kaku{ABC}=120\Deg$

ヒロ

次の角を求める問題では，簡単に図を描いて状況を把握しよう。

【シスの解答】
ADとBCが平行と書かれているから，平行線を2本引く。点Aを上側の直線上にとったときを考えると，点B，Cを下側の直線上に $\kaku{ABC}=120\Deg$, $\mathrm{BC=AB}$ となるようにとる。また，$\mathrm{AB=CD}$ を考えると点Dの位置も決まって，図のようになる。

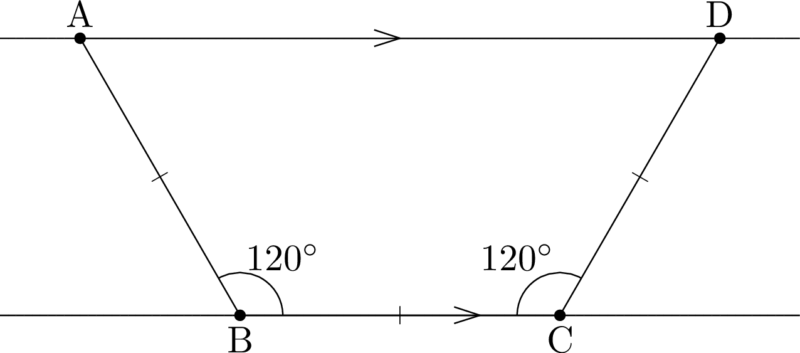
図より，$\kaku{BAD}=\kaku{ADC}=60\Deg$

ヒロ

次はADの長さがBCの何倍かを考える問題。補助線を引くとすぐに求めることができる。

【セ～タの解答】
ADの中点Mと2点B, Cを結ぶと正三角形が3つできる。

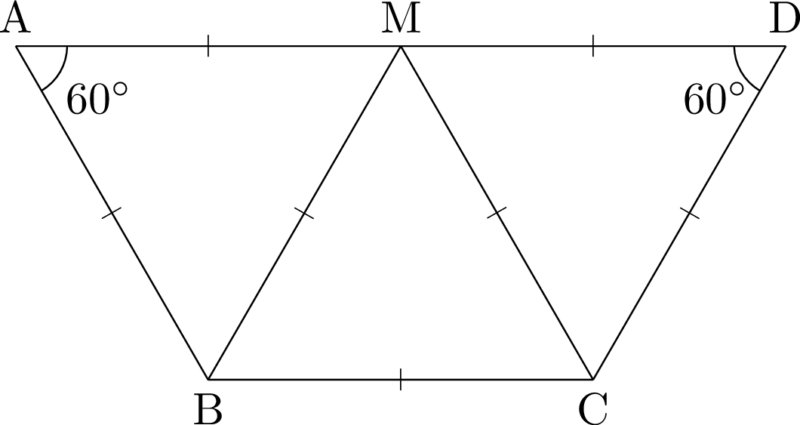
図より，$\Vec{AD}=2\Vec{BC}$ となる。また，

\begin{align*}
\Vec{OD}&=\Vec{OA}+\Vec{AD} \\[4pt]
&=\Vec{OA}+2\Vec{BC} \\[4pt]
&=\vec{a}+2(\vec{c}-\vec{b}) \\[4pt]
&=\vec{a}-2\vec{b}+2\vec{c}
\end{align*}

ヒロ

四角形ABCDの面積は正三角形3つ分の面積に等しい。

正三角形の面積公式一辺の長さが $a$ の正三角形の面積 $S$ は，次のように表される。

\begin{align*}
S=\dfrac{\sqrt3}{4}a^2
\end{align*}

【チツテの解答】
四角形ABCDの面積は

\begin{align*}
\dfrac{\sqrt3}{4}(\sqrt2)^2\times3=\dfrac{3\sqrt{3}}{2}
\end{align*}

(3)の解答

(3) 三角形OACを底面とする三角錐BOACの体積 $V$ を求めよう。
3点O, A, Cの定める平面 $\alpha$ 上に，点Hを $\Vec{BH}\perp\vec{a}$ と $\Vec{BH}\perp\vec{c}$ が成り立つようにとる。$\abs{\Vec{BH}}$ は三角錐BOACの高さである。Hは $\alpha$ 上の点であるから，実数 $s,~t$ を用いて $\Vec{OH}=s\vec{a}+t\vec{c}$ の形に表される。
$\Vec{BH}\Cdot\vec{a}=\myBox{ト}$, $\Vec{BH}\Cdot\vec{c}=\mybox{ト}$ により，$s=\myBox{ナ}$, $t=\dfrac{\myBox{ニ}}{\myBox{ヌ}}$ である。よって，$\abs{\Vec{BH}}=\dfrac{\sqrt{\myBox{ネ}}}{\myBox{ノ}}$ が得られる。したがって，(1)により，$V=\dfrac{\myBox{ハ}}{\myBox{ヒ}}$ であることがわかる。

ヒロ

内積の値を聞かれていて1桁だったら，垂直で0になるんじゃないかと疑おう。

【トの解答】
$\Vec{BH}\perp\vec{a}$, $\Vec{BH}\perp\vec{c}$ より，

\begin{align*}
\Vec{BH}\Cdota\vec{a}=0,~\Vec{BH}\Cdota\vec{c}=0
\end{align*}

ヒロ

$s,~t$ の2文字を求める問題だから，独立した方程式が2本必要。

ヒロ

直前に求めた「内積が0」の2本の方程式を利用しよう。

【ナ～ヌの解答】
$\Vec{BH}\Cdota\vec{a}=0$ より

\begin{align*}
&(\Vec{OH}-\Vec{OB})\Cdota\vec{a}=0 \\[4pt]
&(s\vec{a}+t\vec{c}-\vec{b})\Cdota\vec{a}=0 \\[4pt]
&s\abs{\vec{a}}^2+t\vec{c}\Cdota\vec{a}-\vec{b}\Cdota\vec{a}=0 \\[4pt]
&s-1=0 \\[4pt]
&s=1
\end{align*}

また，$\Vec{BH}\Cdota\vec{c}=0$ より

\begin{align*}
&(\Vec{OH}-\Vec{OB})\Cdota\vec{c}=0 \\[4pt]
&(s\vec{a}+t\vec{c}-\vec{b})\Cdota\vec{c}=0 \\[4pt]
&s\vec{a}\Cdota\vec{c}+t\abs{\vec{c}}^2-\vec{b}\Cdota\vec{c}=0 \\[4pt]
&5t-3=0 \\[4pt]
&t=\dfrac{3}{5}
\end{align*}

ヒロ

次の $\abs{\Vec{BH}}$ を求めるには，2乗してひたすら計算する方法がとられることが多い。

ヒロ

しかし，内積の図形的意味を利用する方が楽な場合もある。

【ネノの解答】

\begin{align*}
\abs{\Vec{BH}}^2&=\Vec{BH}\Cdota\Vec{BA} \\[4pt]
&=\Vec{BH}\Cdota(\vec{a}-\vec{b}) \\[4pt]
&=-\Vec{BH}\Cdota\vec{b} \\[4pt]
&=-\left(\Vec{OH}-\Vec{OB}\right)\Cdota\vec{b} \\[4pt]
&=-\left(\vec{a}+\dfrac{3}{5}\vec{c}-\vec{b}\right)\Cdota\vec{b} \\[4pt]
&=-\vec{a}\Cdota\vec{b}-\dfrac{3}{5}\vec{c}\Cdota\vec{b}+\abs{\vec{b}}^2 \\[4pt]
&=-1-\dfrac{3}{5}\Cdot3+3 \\[4pt]
&=\dfrac{1}{5}
\end{align*}

よって，$\abs{\Vec{BH}}=\dfrac{\sqrt{5}}{5}$

ヒロ

ここまできたら三角錐の体積は大丈夫だろう。

【ハヒの解答】

\begin{align*}
V&=\dfrac{1}{3}\Cdota\sankaku{OAC}\Cdota\abs{\Vec{BH}} \\[4pt]
&=\dfrac{1}{3}\Cdot\dfrac{\sqrt{5}}{2}\Cdot\dfrac{\sqrt{5}}{5} \\[4pt]
&=\dfrac{1}{6}
\end{align*}

(4)の解答

(4) (3)の $V$ を用いると，四角錐OABCDの体積は $\myBox{フ}~V$ と表せる。さらに，四角形ABCDを底面とする四角錐OABCDの高さは $\dfrac{\sqrt{\myBox{ヘ}}}{\myBox{ホ}}$ である。

ヒロ

三角錐BOACの体積 $V$ を用いて，四角錐OABCDの体積を表す問題。BOACとOABCDの文字に着目すると，BOACが共通であることが分かる。3点A, B, Cは同一平面上にあることが分かっているため，これを底面とみる。

【フの解答】
三角形ABCを底面とみた三角錐BOACと四角形ABCDを底面とみた四角錐OABCDの高さが等しくなるから，底面積の比を考えれば良い。

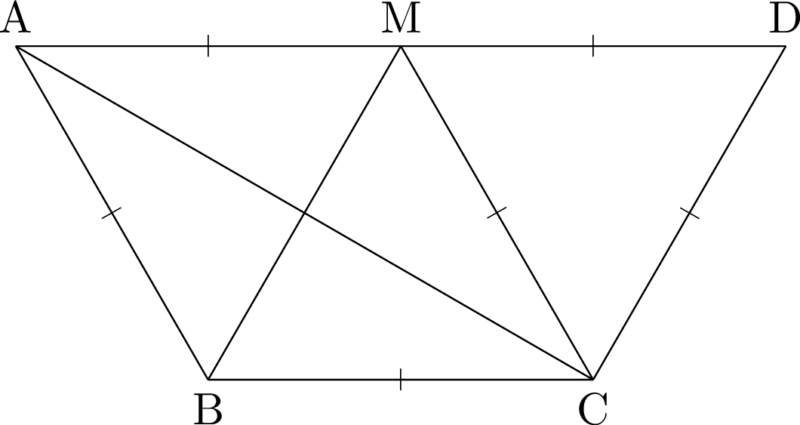
三角形ABCの面積は三角形ABMの面積は等しいから，四角錐OABCDの底面積は三角錐BOACの底面積の3倍となる。よって，

\begin{align*}
(四角錐\mathrm{OABCD}の体積)=3V
\end{align*}

ヒロ

最後は高校入試によく出る考え方だね。1つの立体を着目する底面を変えることで，2通りの方法で体積を表して高さを求める方法を利用しよう。

【ヘホの解答】
求める高さを $h$ とすると

\begin{align*}
&3V=\dfrac{1}{3}\times(四角形\mathrm{ABCD})\times h \\[4pt]
&3\Cdota\dfrac{1}{6}=\dfrac{1}{3}\Cdot\dfrac{3\sqrt{3}}{2}\Cdota h \\[4pt]
&h=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}
\end{align*}