角度を1つに決めることで三角比の値が決まります。
三角定規に現れる30°,45°,60°の三角比の値については,図を描くことで簡単に求めることができます。
また,三角定規の三角形を組み合わせた図形を考えることで,15°や75°の三角比の値も比較的簡単に求めることができます。
様々な角度の三角比の値を求めることで,三角比に慣れていきましょう。
三角定規の角の三角比

ヒロ
三角定規に現れる鋭角は30°,45°,60°であり,それぞれの三角比の値を求めてみよう。
【30°の三角比の値】
まずは30°の三角比の値を考えるために,30°,60°,90°の直角三角形を考える。
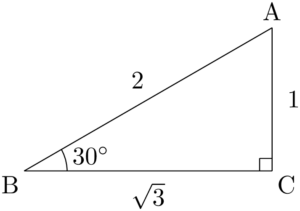
辺の比は
まずは30°の三角比の値を考えるために,30°,60°,90°の直角三角形を考える。

辺の比は
\begin{align*}
\text{CA}:\text{AB}:\text{BC}=1:2:\sqrt{3}
\end{align*}
であるから,\text{CA}:\text{AB}:\text{BC}=1:2:\sqrt{3}
\end{align*}
\begin{align*}
&\sin30\Deg=\dfrac{1}{2} \\[4pt]&\cos30\Deg=\dfrac{\sqrt{3}}{2} \\[4pt]&\tan30\Deg=\dfrac{1}{\sqrt{3}}
\end{align*}
&\sin30\Deg=\dfrac{1}{2} \\[4pt]&\cos30\Deg=\dfrac{\sqrt{3}}{2} \\[4pt]&\tan30\Deg=\dfrac{1}{\sqrt{3}}
\end{align*}

ヒロ
次に60°の三角比の値を求める。
【60°の三角比の値】
60°が左側になるように,三角形の向きを変える。
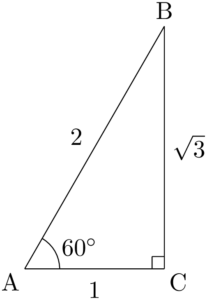
60°が左側になるように,三角形の向きを変える。

\begin{align*}
&\sin60\Deg=\dfrac{\sqrt{3}}{2} \\[4pt]&\cos60\Deg=\dfrac{1}{2} \\[4pt]&\tan60\Deg=\sqrt{3}
\end{align*}
&\sin60\Deg=\dfrac{\sqrt{3}}{2} \\[4pt]&\cos60\Deg=\dfrac{1}{2} \\[4pt]&\tan60\Deg=\sqrt{3}
\end{align*}

ヒロ
最後に45°の三角比の値を求める。
【45°の三角比の値】
45°,45°,90°の直角二等辺三角形を考える。
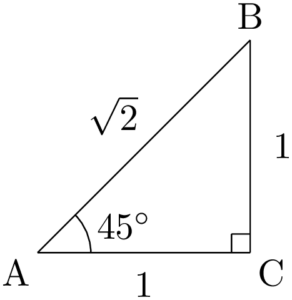
45°,45°,90°の直角二等辺三角形を考える。

\begin{align*}
&\sin45\Deg=\dfrac{1}{\sqrt{2}} \\[4pt]&\cos45\Deg=\dfrac{1}{\sqrt{2}} \\[4pt]&\tan45\Deg=1
\end{align*}
&\sin45\Deg=\dfrac{1}{\sqrt{2}} \\[4pt]&\cos45\Deg=\dfrac{1}{\sqrt{2}} \\[4pt]&\tan45\Deg=1
\end{align*}
75°の三角比

ヒロ
三角定規の三角形の組み合わせを考えて75°の三角比の値を求めてみよう。
【75°の三角比の値】
$1:2:\sqrt{3}$ の直角三角形と $1:1:\sqrt{2}$ の直角三角形を組み合わせた次の図を考える。
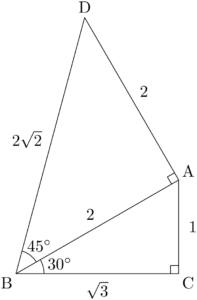
$\kaku{DBC}=75\Deg$ であるから,点Dから辺BCに垂線DHを下ろして直角三角形を考える。
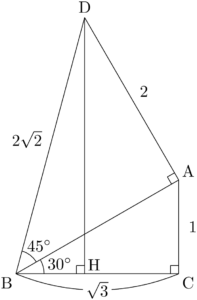
BHとDHの長さを求めるために,点AからDHに垂線AEを下ろす。
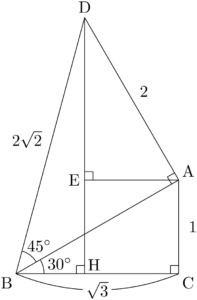
AEとBCが平行であるから,$\kaku{BAE}=30\Deg$ である。よって,$\kaku{DAE}=60\Deg$ である。
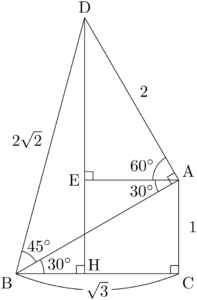
$\sankaku{ADE}$ は $1:2:\sqrt{3}$ の直角三角形であるから,$\text{DE}=\sqrt{3}$ であり,$\text{AE}=1$ である。したがって,$\text{CH}=1$ となるから,
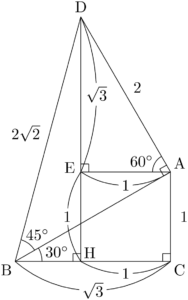
これで三角形BDHの3辺の長さが分かったことになる。
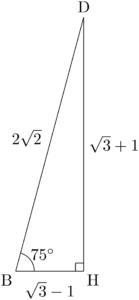
これより
$1:2:\sqrt{3}$ の直角三角形と $1:1:\sqrt{2}$ の直角三角形を組み合わせた次の図を考える。

$\kaku{DBC}=75\Deg$ であるから,点Dから辺BCに垂線DHを下ろして直角三角形を考える。

BHとDHの長さを求めるために,点AからDHに垂線AEを下ろす。

AEとBCが平行であるから,$\kaku{BAE}=30\Deg$ である。よって,$\kaku{DAE}=60\Deg$ である。

$\sankaku{ADE}$ は $1:2:\sqrt{3}$ の直角三角形であるから,$\text{DE}=\sqrt{3}$ であり,$\text{AE}=1$ である。したがって,$\text{CH}=1$ となるから,
\begin{align*}
&\text{BH}=\text{BC}-\text{CH}=\sqrt{3}-1 \\[4pt]&\text{DH}=\text{DE}+\text{EH}=\sqrt{3}+1
\end{align*}
&\text{BH}=\text{BC}-\text{CH}=\sqrt{3}-1 \\[4pt]&\text{DH}=\text{DE}+\text{EH}=\sqrt{3}+1
\end{align*}

これで三角形BDHの3辺の長さが分かったことになる。
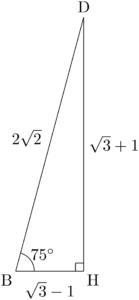
これより
\begin{align*}
&\sin75\Deg=\dfrac{\sqrt{3}+1}{2\sqrt{2}}=\dfrac{\sqrt{6}+\sqrt{2}}{4} \\[4pt]&\cos75\Deg=\dfrac{\sqrt{3}-1}{2\sqrt{2}}=\dfrac{\sqrt{6}-\sqrt{2}}{4} \\[4pt]&\tan75\Deg=\dfrac{\sqrt{3}+1}{\sqrt{3}-1}=2+\sqrt{3}
\end{align*}
&\sin75\Deg=\dfrac{\sqrt{3}+1}{2\sqrt{2}}=\dfrac{\sqrt{6}+\sqrt{2}}{4} \\[4pt]&\cos75\Deg=\dfrac{\sqrt{3}-1}{2\sqrt{2}}=\dfrac{\sqrt{6}-\sqrt{2}}{4} \\[4pt]&\tan75\Deg=\dfrac{\sqrt{3}+1}{\sqrt{3}-1}=2+\sqrt{3}
\end{align*}
15°の三角比

ヒロ
15°の三角比の値は簡単に求めることができるね。
【15°の三角比の値】
$\kaku{BDH}=90\Deg-75\Deg=15\Deg$ であるから,上で作った三角形BDHの15°が左に来るように向きを変えると次のようになる。
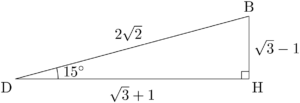
したがって
$\kaku{BDH}=90\Deg-75\Deg=15\Deg$ であるから,上で作った三角形BDHの15°が左に来るように向きを変えると次のようになる。

したがって
\begin{align*}
&\sin15\Deg=\dfrac{\sqrt{3}-1}{2\sqrt{2}}=\dfrac{\sqrt{6}-\sqrt{2}}{4} \\[4pt]&\cos15\Deg=\dfrac{\sqrt{3}+1}{2\sqrt{2}}=\dfrac{\sqrt{6}+\sqrt{2}}{4} \\[4pt]&\tan15\Deg=\dfrac{\sqrt{3}-1}{\sqrt{3}+1}=2-\sqrt{3}
\end{align*}
&\sin15\Deg=\dfrac{\sqrt{3}-1}{2\sqrt{2}}=\dfrac{\sqrt{6}-\sqrt{2}}{4} \\[4pt]&\cos15\Deg=\dfrac{\sqrt{3}+1}{2\sqrt{2}}=\dfrac{\sqrt{6}+\sqrt{2}}{4} \\[4pt]&\tan15\Deg=\dfrac{\sqrt{3}-1}{\sqrt{3}+1}=2-\sqrt{3}
\end{align*}
15°と75°の三角比

ヒロ
別の考え方として,次のようなものもある。
【15°と75°の三角比】
まず,15°,75°,90°の直角三角形ABCを描こう。

辺ABの垂直二等分線とBCの交点をDとすると,$\text{AD}=\text{BD}$ となる。
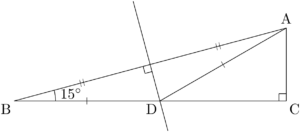
三角形ABDは底角15°の二等辺三角形であるから,$\kaku{CDA}=30\Deg$ となる。
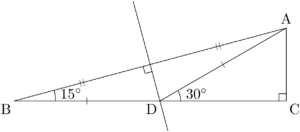
$\text{AC}=1$ とすると,$\text{CD}=\sqrt{3}$, $\text{AD}=\text{BD}=2$ となる。
三平方の定理より

図より,15°と75°の三角比の値を求めることができる。
まず,15°,75°,90°の直角三角形ABCを描こう。

辺ABの垂直二等分線とBCの交点をDとすると,$\text{AD}=\text{BD}$ となる。

三角形ABDは底角15°の二等辺三角形であるから,$\kaku{CDA}=30\Deg$ となる。

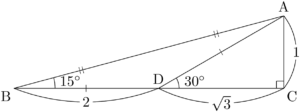
$\text{AC}=1$ とすると,$\text{CD}=\sqrt{3}$, $\text{AD}=\text{BD}=2$ となる。

三平方の定理より
\begin{align*}
\text{AB}&=\sqrt{(2+\sqrt{3})^2+1} \\[4pt]&=\sqrt{8+4\sqrt{3}} \\[4pt]&=\sqrt{8+2\sqrt{12}} \\[4pt]&=\sqrt{6}+\sqrt{2}
\end{align*}
となるから,三角形ABCの3辺の長さは次のようになる。\text{AB}&=\sqrt{(2+\sqrt{3})^2+1} \\[4pt]&=\sqrt{8+4\sqrt{3}} \\[4pt]&=\sqrt{8+2\sqrt{12}} \\[4pt]&=\sqrt{6}+\sqrt{2}
\end{align*}

図より,15°と75°の三角比の値を求めることができる。

ヒロ
途中で二重根号を外す作業が必要になる。

ヒロ
二重根号の外し方については次の記事で説明しているので,考え方を忘れている人は復習しておこう。
22.5°と67.5°の三角比の値

ヒロ
同じようにして22.5°と67.5°の三角比の値も求めることができる。
【22.5°と67.5°の三角比の値】
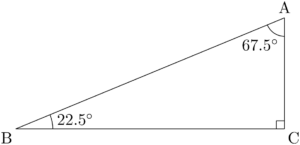
まず,22.5°,67.5°,90°の直角三角形ABCを描こう。
辺ABの垂直二等分線とBCの交点をDとすると,$\text{AD}=\text{BD}$ となる。
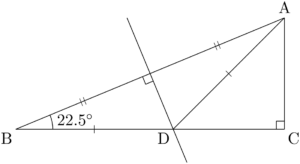
三角形ABDは底角22.5°の二等辺三角形であるから,$\kaku{CDA}=45\Deg$ となる。
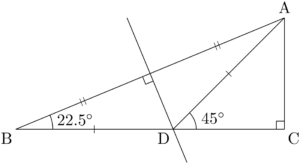
$\text{AC}=1$ とすると,$\text{CD}=1$, $\text{AD}=\text{BD}=\sqrt{2}$ となる。
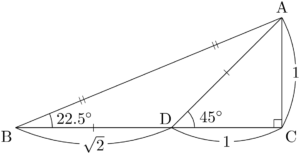
三平方の定理より
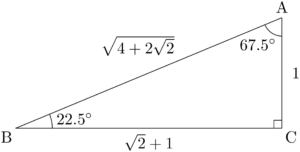
※この二重根号を外すことはできない。
したがって

まず,22.5°,67.5°,90°の直角三角形ABCを描こう。

辺ABの垂直二等分線とBCの交点をDとすると,$\text{AD}=\text{BD}$ となる。

三角形ABDは底角22.5°の二等辺三角形であるから,$\kaku{CDA}=45\Deg$ となる。

$\text{AC}=1$ とすると,$\text{CD}=1$, $\text{AD}=\text{BD}=\sqrt{2}$ となる。

三平方の定理より
\begin{align*}
\text{AB}&=\sqrt{(\sqrt{2}+1)^2+1} \\[4pt]&=\sqrt{4+2\sqrt{2}}
\end{align*}
となるから,三角形ABCの3辺の長さは次のようになる。\text{AB}&=\sqrt{(\sqrt{2}+1)^2+1} \\[4pt]&=\sqrt{4+2\sqrt{2}}
\end{align*}

※この二重根号を外すことはできない。
したがって
\begin{align*}
\sin22.5\Deg&=\dfrac{1}{\sqrt{4+2\sqrt{2}}}=\dfrac{1}{\sqrt{2}\sqrt{2+\sqrt{2}}} \\[4pt]&=\dfrac{\sqrt{2-\sqrt{2}}}{\sqrt{2}\sqrt{2+\sqrt{2}}\sqrt{2-\sqrt{2}}} \\[4pt]&=\dfrac{\sqrt{2-\sqrt{2}}}{2} \\[4pt]\cos22.5\Deg&=\dfrac{\sqrt{2}+1}{\sqrt{4+2\sqrt{2}}}
=\dfrac{(\sqrt{2}+1)\sqrt{2-\sqrt{2}}}{2} \\[4pt]&=\dfrac{\sqrt{(3+2\sqrt{2})(2-\sqrt{2})}}{2} \\[4pt]&=\dfrac{\sqrt{2+\sqrt{2}}}{2} \\[4pt]\tan22.5\Deg&=\dfrac{1}{\sqrt{2}+1}=\sqrt{2}-1
\end{align*}
67.5°の三角比の値も次の図から求めることができる。\sin22.5\Deg&=\dfrac{1}{\sqrt{4+2\sqrt{2}}}=\dfrac{1}{\sqrt{2}\sqrt{2+\sqrt{2}}} \\[4pt]&=\dfrac{\sqrt{2-\sqrt{2}}}{\sqrt{2}\sqrt{2+\sqrt{2}}\sqrt{2-\sqrt{2}}} \\[4pt]&=\dfrac{\sqrt{2-\sqrt{2}}}{2} \\[4pt]\cos22.5\Deg&=\dfrac{\sqrt{2}+1}{\sqrt{4+2\sqrt{2}}}
=\dfrac{(\sqrt{2}+1)\sqrt{2-\sqrt{2}}}{2} \\[4pt]&=\dfrac{\sqrt{(3+2\sqrt{2})(2-\sqrt{2})}}{2} \\[4pt]&=\dfrac{\sqrt{2+\sqrt{2}}}{2} \\[4pt]\tan22.5\Deg&=\dfrac{1}{\sqrt{2}+1}=\sqrt{2}-1
\end{align*}

\begin{align*}
&\sin67.5\Deg=\dfrac{\sqrt{2}+1}{\sqrt{4+2\sqrt{2}}}=\dfrac{\sqrt{2+\sqrt{2}}}{2} \\[4pt]&\cos67.5\Deg=\dfrac{1}{\sqrt{4+2\sqrt{2}}}=\dfrac{\sqrt{2-\sqrt{2}}}{2} \\[4pt]&\tan67.5\Deg=\sqrt{2}+1
\end{align*}
&\sin67.5\Deg=\dfrac{\sqrt{2}+1}{\sqrt{4+2\sqrt{2}}}=\dfrac{\sqrt{2+\sqrt{2}}}{2} \\[4pt]&\cos67.5\Deg=\dfrac{1}{\sqrt{4+2\sqrt{2}}}=\dfrac{\sqrt{2-\sqrt{2}}}{2} \\[4pt]&\tan67.5\Deg=\sqrt{2}+1
\end{align*}
鋭角の三角比の値

ヒロ
三角定規に現れる角とそれらの組合せによって得られる鋭角の三角比の値をまとめると次のようになる。
鋭角の三角比の値
- $\sin15\Deg=\dfrac{\sqrt{6}-\sqrt{2}}{4}$
- $\cos15\Deg=\dfrac{\sqrt{6}+\sqrt{2}}{4}$
- $\tan15\Deg=2-\sqrt{3}$
- $\sin22.5\Deg=\dfrac{\sqrt{2-\sqrt{2}}}{2}$
- $\cos22.5\Deg=\dfrac{\sqrt{2+\sqrt{2}}}{2}$
- $\tan22.5\Deg=\sqrt{2}-1$
- $\sin30\Deg=\dfrac{1}{2}$
- $\cos30\Deg=\dfrac{\sqrt{3}}{2}$
- $\tan30\Deg=\dfrac{1}{\sqrt{3}}$
- $\sin45\Deg=\dfrac{1}{\sqrt{2}}$
- $\cos45\Deg=\dfrac{1}{\sqrt{2}}$
- $\tan45\Deg=1$
- $\sin60\Deg=\dfrac{\sqrt{3}}{2}$
- $\cos60\Deg=\dfrac{1}{2}$
- $\tan60\Deg=\sqrt{3}$
- $\sin67.5\Deg=\dfrac{\sqrt{2+\sqrt{2}}}{2}$
- $\cos67.5\Deg=\dfrac{\sqrt{2-\sqrt{2}}}{2}$
- $\tan67.5\Deg=\sqrt{2}+1$
- $\sin75\Deg=\dfrac{\sqrt{6}+\sqrt{2}}{4}$
- $\cos75\Deg=\dfrac{\sqrt{6}-\sqrt{2}}{4}$
- $\tan75\Deg=2+\sqrt{3}$





















