2つの放物線の共通接線を簡単に求める方法【マーク式試験で速答できる】

2つの放物線の共通接線を求める問題では，微分を用いて求める方法がよくある解法です。

しかし，放物線の性質を利用することで，簡単に2つの放物線の共通接線を求めることができます。放物線の「2乗に比例する性質」を理解していることが必須なので，お手数ですが次の記事を先に読んでください。

【微分不要】放物線上にない点から放物線に引いた接線を簡単に求める方法

微分を用いずに，放物線上にない点から引いた接線の方程式を求める方法を説明します。2次関数がもつ「2乗に比例する性質」を利用することで，それが可能になります。また，2次関数のグラフについて深く理解することで，今までとは異なる視点をもつことができるようになります。

methodology.site

2019.09.28

$x^2$ の係数が等しい2つの放物線の共通接線

ヒロ

まずは $x^2$ の係数が等しい2つの放物線の共通接線を考えよう。

放物線 $C, D$ の $x^2$ の係数が等しいとき，一方のグラフを平行移動すると，もう一方のグラフに重なる状態になっている。$C, D$ の頂点をそれぞれP, Qとすると，$C$ 上のすべての点は $\Vec{PQ}$ だけ平行移動された点に移り，$D$ を描く。

ヒロ

2つの放物線の共通接線を描くと次のようになる。

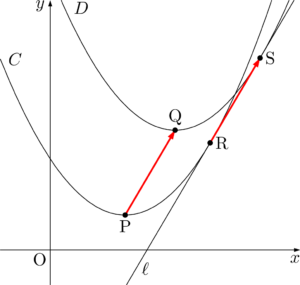
共通接線 $\ell$ と2つの放物線 $C,~D$ の接点をそれぞれR, Sとすると，

\begin{align*}
\Vec{RS}=\Vec{PQ}
\end{align*}

が成り立つことが分かるだろう。つまり，$x^2$ の係数が等しい2つの放物線の共通接線は，2つの頂点を通る直線と平行である。