カージオイド曲線（媒介変数表示・弧長・面積・体積）

Contents

カージオイド曲線の描画

ヒロ

媒介変数表示された関数のグラフを描こう。

$\displaystyle
f(\theta)=a\cos\theta(1+\cos\theta),~g(\theta)=a\sin\theta(1+\cos\theta)
$

とおく。

\begin{align*}
f(2\pi-\theta)&=a\cos(2\pi-\theta)\{1+\cos(2\pi-\theta)\} \\[4pt]&=a\cos\theta(1+\cos\theta) \\[4pt]&=f(\theta) \\[4pt]g(2\pi-\theta)&=a\sin(2\pi-\theta)\{1+\cos(2\pi-\theta)\} \\[4pt]&=-a\sin\theta(1+\cos\theta) \\[4pt]&=-g(\theta)
\end{align*}

となるから，$0\leqq\theta\leqq\pi$ の部分と $\pi\leqq\theta\leqq2\pi$ の部分は $x$ 軸に関して対称である。
したがって，$0\leqq\theta\leqq\pi$ において考える。
$\begin{cases}
x=a\cos\theta(1+\cos\theta) \\[4pt]y=a\sin\theta(1+\cos\theta)
\end{cases}$より，

\begin{align*}
\dfrac{dx}{d\theta}&=a(-\sin\theta-2\cos\theta\sin\theta) \\[4pt]&=-a(\sin\theta+\sin2\theta) \\[4pt]\dfrac{dy}{d\theta}&=a(\cos\theta+\cos^2\theta-\sin^2\theta) \\[4pt]&=a(\cos\theta+\cos2\theta)
\end{align*}

$\dfrac{dx}{d\theta}=0$ とすると，

\begin{align*}
&\sin\theta+\sin2\theta=0 \\[4pt]&\sin\theta(1+2\cos\theta)=0 \\[4pt]&\sin\theta=0~~または~\cos\theta=-\dfrac{1}{2} \\[4pt]&\theta=0,~\dfrac23\pi,~\pi
\end{align*}

$\dfrac{dy}{d\theta}=0$ とすると，

\begin{align*}
&\cos\theta+\cos2\theta=0 \\[4pt]&2\cos^2\theta+\cos\theta-1=0 \\[4pt]&(\cos\theta+1)(2\cos\theta-1)=0 \\[4pt]&\cos\theta=-1,~\dfrac{1}{2} \\[4pt]&\theta=\dfrac{\pi}{3},~\pi
\end{align*}

よって，増減は次のようになる。

\begin{align*}
\def\arraystretch{1.3}
\begin{array}{|c||c|c|c|c|c|c|c|}\hline
\theta & 0 & \cdots & \dfrac{\pi}{3} & \cdots &
\dfrac23\pi & \cdots & \pi \\\hline
\dfrac{dx}{d\theta} & 0 & – & – & – & 0 & + & 0 \\\hline
\dfrac{dy}{d\theta} & 0 & + & 0 & – & – & – & 0 \\\hline
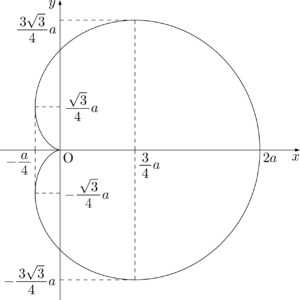
(x,~y) & (2a,~0) & \nwarrow & \left(\dfrac34a,~\dfrac{3\sqrt3}{4}a\right)
& \swarrow & \left(-\dfrac{a}{4},~\dfrac{\sqrt3}{4}a\right) & \searrow & (0,~0) \\\hline
\end{array}
\end{align*}

よって，カージオイドのグラフは図のようになる。