Contents
カージオイド曲線の回転体の体積

ヒロ
カージオイド曲線で囲まれる部分を $x$ 軸のまわりに1回転してできる立体の体積 $V$ を求めよう。
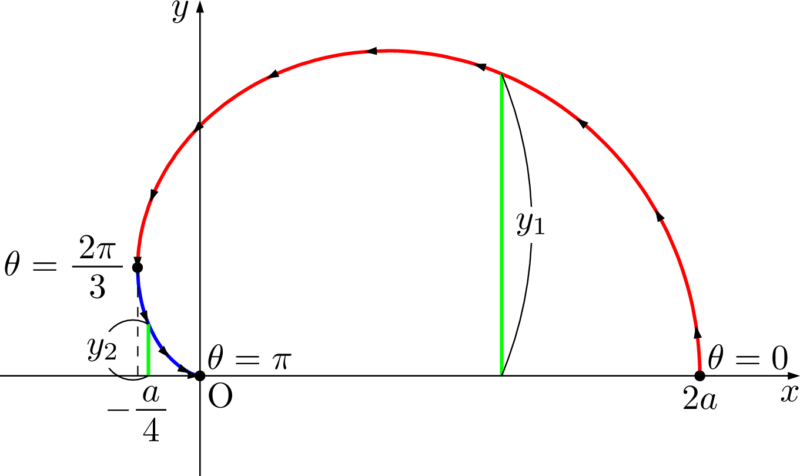
求める体積は $0\leqq\theta\leqq\dfrac23\pi$ の部分(赤線)を $x$ 軸のまわりに1回転してできる立体の体積から,$\dfrac23\pi\leqq\theta\leqq\pi$ の部分(青線)を $x$ 軸のまわりに1回転してできる立体の体積を引いたものである。

\begin{align*}
V&=\dint{-\frac14a}{2a}\pi{y_1}^2\;dx-\dint{-\frac14a}{0}\pi{y_2}^2\;dx \\
&=\dint{\frac23\pi}{0}\pi y^2\dfrac{dx}{d\theta}\;d\theta
-\dint{\frac23\pi}{\pi}\pi y^2\dfrac{dx}{d\theta}\;d\theta \\
&=\dint{\pi}{0}\pi y^2\dfrac{dx}{d\theta}\;d\theta \\
&=\pi\dint{\pi}{0}a^2\sin^2\theta(1+\cos\theta)^2\cdot
a(-\sin\theta-2\cos\theta\sin\theta)\;d\theta \\
&=\pi a^3\dint{0}{\pi}\sin^3\theta(1+\cos\theta)^2(1+2\cos\theta)\;d\theta \\
&=\pi a^3\dint{0}{\pi}(1-\cos^2\theta)(1+\cos\theta)^2(1+2\cos\theta)\sin\theta\;d\theta \\
&=\pi a^3\dint{0}{\pi}(2\cos^5\theta+5\cos^4\theta+2\cos^3\theta-4\cos^2\theta
-4\cos\theta-1)(\cos\theta)’\;d\theta \\
&=\pi a^3\Tint{\dfrac13\cos^6\theta+\cos^5\theta+\dfrac12\cos^4\theta
-\dfrac43\cos^3\theta-2\cos^2\theta-\cos\theta}{0}{\pi} \\
&=\pi a^3\left\{\dfrac{1-1}{3}+(-1-1)+\dfrac{1-1}{2}-\dfrac43(-1-1)-2(1-1)-(-1-1)\right\} \\
&=\dfrac83\pi a^3
\end{align*}
V&=\dint{-\frac14a}{2a}\pi{y_1}^2\;dx-\dint{-\frac14a}{0}\pi{y_2}^2\;dx \\
&=\dint{\frac23\pi}{0}\pi y^2\dfrac{dx}{d\theta}\;d\theta
-\dint{\frac23\pi}{\pi}\pi y^2\dfrac{dx}{d\theta}\;d\theta \\
&=\dint{\pi}{0}\pi y^2\dfrac{dx}{d\theta}\;d\theta \\
&=\pi\dint{\pi}{0}a^2\sin^2\theta(1+\cos\theta)^2\cdot
a(-\sin\theta-2\cos\theta\sin\theta)\;d\theta \\
&=\pi a^3\dint{0}{\pi}\sin^3\theta(1+\cos\theta)^2(1+2\cos\theta)\;d\theta \\
&=\pi a^3\dint{0}{\pi}(1-\cos^2\theta)(1+\cos\theta)^2(1+2\cos\theta)\sin\theta\;d\theta \\
&=\pi a^3\dint{0}{\pi}(2\cos^5\theta+5\cos^4\theta+2\cos^3\theta-4\cos^2\theta
-4\cos\theta-1)(\cos\theta)’\;d\theta \\
&=\pi a^3\Tint{\dfrac13\cos^6\theta+\cos^5\theta+\dfrac12\cos^4\theta
-\dfrac43\cos^3\theta-2\cos^2\theta-\cos\theta}{0}{\pi} \\
&=\pi a^3\left\{\dfrac{1-1}{3}+(-1-1)+\dfrac{1-1}{2}-\dfrac43(-1-1)-2(1-1)-(-1-1)\right\} \\
&=\dfrac83\pi a^3
\end{align*}
極方程式と体積
極方程式 $r=f(\theta)$ で表される曲線と2直線 $\theta=\alpha$, $\theta=\beta$ で囲まれる部分を始線のまわりに1回転して得られる立体の体積を $V$ とすると
\begin{align*}
V=\dint{\alpha}{\beta}\dfrac{2}{3}\pi\{f(\theta)\}^3\sin\theta\;d\theta
\end{align*}
V=\dint{\alpha}{\beta}\dfrac{2}{3}\pi\{f(\theta)\}^3\sin\theta\;d\theta
\end{align*}

ヒロ
この公式を使って,体積 $V$ を求めてみよう。
$f(\theta)=a(1+\cos\theta)$ より
\begin{align*}
V&=\dint{0}{\pi}\dfrac{2}{3}\pi a^3(1+\cos\theta)^3\sin\theta\;d\theta \\[4pt]
&=\dfrac{2}{3}\pi a^3\dint{0}{\pi}(1+3\cos\theta+3\cos^2\theta+\cos^3\theta)\sin\theta\;d\theta \\[4pt]
&=\dfrac{2}{3}\pi a^3\Tint{-\cos\theta-\dfrac{3}{2}\cos^2\theta-\cos^3\theta-\dfrac{1}{4}\cos^4\theta}{0}{\pi} \\[4pt]
&=\dfrac{2}{3}\pi a^3\left\{2-\dfrac{3}{2}(1-1)-(-1-1)-\dfrac{1}{4}(1-1)\right\} \\[4pt]
&=\dfrac{8}{3}\pi a^3
\end{align*}
V&=\dint{0}{\pi}\dfrac{2}{3}\pi a^3(1+\cos\theta)^3\sin\theta\;d\theta \\[4pt]
&=\dfrac{2}{3}\pi a^3\dint{0}{\pi}(1+3\cos\theta+3\cos^2\theta+\cos^3\theta)\sin\theta\;d\theta \\[4pt]
&=\dfrac{2}{3}\pi a^3\Tint{-\cos\theta-\dfrac{3}{2}\cos^2\theta-\cos^3\theta-\dfrac{1}{4}\cos^4\theta}{0}{\pi} \\[4pt]
&=\dfrac{2}{3}\pi a^3\left\{2-\dfrac{3}{2}(1-1)-(-1-1)-\dfrac{1}{4}(1-1)\right\} \\[4pt]
&=\dfrac{8}{3}\pi a^3
\end{align*}
まとめ

ヒロ
カージオイド曲線についてまとめると次のようになる。
カージオイド曲線
- グラフの概形
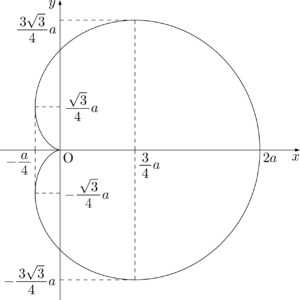
- 媒介変数表示\begin{align*}
x=a\cos\theta(1+\cos\theta),~~y=a\sin\theta(1+\cos\theta)
\end{align*} - 極方程式\begin{align*}
r=a(1+\cos\theta)
\end{align*} - 面積\begin{align*}
S=\dfrac{3}{2}\pi a^2
\end{align*} - 曲線の長さ\begin{align*}
L=8a
\end{align*} - 回転体の体積\begin{align*}
V=\dfrac{8}{3}\pi a^3
\end{align*}


















