定積分の計算について解説します。
定積分の計算は,面積や体積を求めるのに役に立ちますが,まずは定積分の計算方法を知り,正しく速く計算できるようにすることが重要です。
定積分とは

ヒロ
まずは定積分の計算方法を知ろう。
定積分$F'(x)=f(x)$ のとき
\begin{align*}
\dint{a}{b}f(x)\;dx&=\tint{F(x)}{a}{b} \\[4pt]
&=F(b)-F(a)
\end{align*}
定積分を求める区間 $a\leqq x\leqq b$ を積分区間という。\dint{a}{b}f(x)\;dx&=\tint{F(x)}{a}{b} \\[4pt]
&=F(b)-F(a)
\end{align*}
2016年 千葉工業大
2016年 千葉工業大$\dint{-2}{1}(x^3-3x+2)\;dx=\dfrac{\myhako}{\myhako}$ である。
【解答と考え方】
\begin{align*}
&\dint{-2}{1}(x^3-3x+2)\;dx \\[4pt]
&=\tint{\dfrac{1}{4}x^4-\dfrac{3}{2}x^2+2x}{-2}{1} \\[4pt]
&=\dfrac{1-16}{4}-\dfrac{3}{2}(1-4)+2(1+2) \\[4pt]
&=-\dfrac{15}{4}+\dfrac{9}{2}+6 \\[4pt]
&=\dfrac{-15+18+24}{4} \\[4pt]
&=\dfrac{27}{4}
\end{align*}
&\dint{-2}{1}(x^3-3x+2)\;dx \\[4pt]
&=\tint{\dfrac{1}{4}x^4-\dfrac{3}{2}x^2+2x}{-2}{1} \\[4pt]
&=\dfrac{1-16}{4}-\dfrac{3}{2}(1-4)+2(1+2) \\[4pt]
&=-\dfrac{15}{4}+\dfrac{9}{2}+6 \\[4pt]
&=\dfrac{-15+18+24}{4} \\[4pt]
&=\dfrac{27}{4}
\end{align*}

ヒロ
上端と下端を代入して数値計算をする前に,微分して元に戻ることを確認すると良い。

ヒロ
もし積分した時点で間違っていたなら,その後の数値計算をする時間も労力も無駄になる。できればそうした無駄を排除しよう。
2021年 大阪工業大
2021年 大阪工業大定積分 $\dint{1}{2}(x-a)^2\;dx$ を計算せよ。

ヒロ
被積分関数を展開して定積分を計算することもできるが,次のことを覚えておくのが良い。
積分の基本公式$a\neq0$,$n$ を自然数とするとき,
\begin{align*}
\dint{}{}(ax+b)^n\;dx=\dfrac{1}{a}\Cdota\dfrac{(ax+b)^{n+1}}{n+1}+C(Cは積分定数)
\end{align*}
\dint{}{}(ax+b)^n\;dx=\dfrac{1}{a}\Cdota\dfrac{(ax+b)^{n+1}}{n+1}+C(Cは積分定数)
\end{align*}
【解答と考え方】
\begin{align*}
&\dint{1}{2}(x-a)^2\;dx \\[4pt]
&=\Tint{\dfrac{1}{3}(x-a)^3}{1}{2} \\[4pt]
&=\dfrac{(2-a)^3-(1-a)^3}{3} \\[4pt]
&=\dfrac{(8-12a+6a^2-a^3)-(1-3a+3a^2-a^3)}{3} \\[4pt]
&=a^2-3a+\dfrac{7}{3}
\end{align*}
&\dint{1}{2}(x-a)^2\;dx \\[4pt]
&=\Tint{\dfrac{1}{3}(x-a)^3}{1}{2} \\[4pt]
&=\dfrac{(2-a)^3-(1-a)^3}{3} \\[4pt]
&=\dfrac{(8-12a+6a^2-a^3)-(1-3a+3a^2-a^3)}{3} \\[4pt]
&=a^2-3a+\dfrac{7}{3}
\end{align*}
2021年 学習院大
2021年 学習院大積分 $\dint{-1}{2}\abs{x^3-3x}\;dx$ を求めよ。
【解答と考え方】
絶対値記号を外すために,絶対値記号の中身が0以上になる $x$ の値の範囲を求めよう。$x^3-3x\geqq0$ を解くために,$y=x^3-3x$ のグラフを考える。厳密なグラフでなく,$x$ 軸との交点と $x$ 軸との上下関係が分かればよい。このグラフと $x$ 軸との交点を求めるために,$y=0$ とすると,
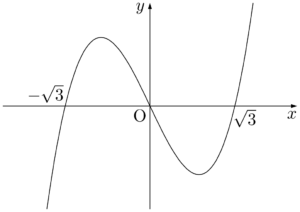
グラフより,$x^3-3x\geqq0$ の解は $-\sqrt{3}\leqq x\leqq0$,$\sqrt{3}\leqq x$
積分区間は $-1\leqq x\leqq2$ であるから
絶対値記号を外すために,絶対値記号の中身が0以上になる $x$ の値の範囲を求めよう。$x^3-3x\geqq0$ を解くために,$y=x^3-3x$ のグラフを考える。厳密なグラフでなく,$x$ 軸との交点と $x$ 軸との上下関係が分かればよい。このグラフと $x$ 軸との交点を求めるために,$y=0$ とすると,
\begin{align*}
&x(x^2-3)=0 \\[4pt]
&x=0,~\pm\sqrt{3}
\end{align*}
$x^3$ の係数が正であることから,$y=x^3-3x$ のグラフは次のようになる。&x(x^2-3)=0 \\[4pt]
&x=0,~\pm\sqrt{3}
\end{align*}

グラフより,$x^3-3x\geqq0$ の解は $-\sqrt{3}\leqq x\leqq0$,$\sqrt{3}\leqq x$
積分区間は $-1\leqq x\leqq2$ であるから
\begin{align*}
\abs{x^3-3x}=
\begin{cases}
x^3-3x &~(-1\leqq x\leqq0,~\sqrt{3}\leqq x\leqq2) \\[4pt]
-x^3+3x &~(0\leqq x\leqq\sqrt{3})
\end{cases}
\end{align*}
となる。したがって\abs{x^3-3x}=
\begin{cases}
x^3-3x &~(-1\leqq x\leqq0,~\sqrt{3}\leqq x\leqq2) \\[4pt]
-x^3+3x &~(0\leqq x\leqq\sqrt{3})
\end{cases}
\end{align*}
\begin{align*}
&\dint{-1}{2}\abs{x^3-3x}\;dx \\[4pt]
&=\dint{-1}{0}(x^3-3x)\;dx+\dint{0}{\sqrt{3}}(-x^3+3x)\;dx+\dint{\sqrt{3}}{2}(x^3-3x)\;dx \\[4pt]
&=\Tint{\dfrac{1}{4}x^4-\dfrac{3}{2}x^2}{-1}{0}+\Tint{-\dfrac{1}{4}x^4+\dfrac{3}{2}x^2}{0}{\sqrt{3}}+\Tint{\dfrac{1}{4}x^4-\dfrac{3}{2}x^2}{\sqrt{3}}{2} \\[4pt]
&=-\dfrac{1}{4}+\dfrac{3}{2}-\dfrac{9}{4}+\dfrac{9}{2}+\dfrac{16-9}{4}-\dfrac{3}{2}(4-3) \\[4pt]
&=\dfrac{-1-9+7}{4}+\dfrac{3+9-3}{2} \\[4pt]
&=-\dfrac{3}{4}+\dfrac{9}{2}=\dfrac{15}{4}
\end{align*}
&\dint{-1}{2}\abs{x^3-3x}\;dx \\[4pt]
&=\dint{-1}{0}(x^3-3x)\;dx+\dint{0}{\sqrt{3}}(-x^3+3x)\;dx+\dint{\sqrt{3}}{2}(x^3-3x)\;dx \\[4pt]
&=\Tint{\dfrac{1}{4}x^4-\dfrac{3}{2}x^2}{-1}{0}+\Tint{-\dfrac{1}{4}x^4+\dfrac{3}{2}x^2}{0}{\sqrt{3}}+\Tint{\dfrac{1}{4}x^4-\dfrac{3}{2}x^2}{\sqrt{3}}{2} \\[4pt]
&=-\dfrac{1}{4}+\dfrac{3}{2}-\dfrac{9}{4}+\dfrac{9}{2}+\dfrac{16-9}{4}-\dfrac{3}{2}(4-3) \\[4pt]
&=\dfrac{-1-9+7}{4}+\dfrac{3+9-3}{2} \\[4pt]
&=-\dfrac{3}{4}+\dfrac{9}{2}=\dfrac{15}{4}
\end{align*}