前回説明した「二項係数の和」も有名な公式の1つであり,入試でよく出題される問題です。今回の記事では,二項係数の有名な3つの公式について説明します。
いずれも重要な公式であり,より複雑な問題の基礎ともなります。
したがって,いつでも扱えるようにしましょう。証明できるのは当然として,その結果も覚えましょう。また,覚えやすくするために,捉え方についても説明します。
&(1)\ \nCk{n}{k}=\nCk{n}{n-k} \\[4pt]
&(2)\ \nCk{n}{k}=\nCk{n-1}{k-1}+\nCk{n-1}{k} \\[4pt]
&(3)\ k\,\nCk{n}{k}=n\,\nCk{n-1}{k-1}
\end{align*}
Contents
二項係数 $\nCk{n}{k}$ の計算方法

まずは,二項係数 $\nCk{n}{k}$ の計算方法について復習しておこう。階乗を用いて表せるかな?

$\nCk{n}{k}=\dfrac{n!}{k!(n-k)!}$ ですよね!

そうだね!文字が少し変わると全く使えなくなる人は,次のような式で頭に入れても構わない。$\nCk{\color{blue}{●}}{\color{green}{●}}=\dfrac{{\color{blue}{●}}!}{{\color{green}{●}}!({\color{blue}{●}}-{\color{green}{●}})!}$
$\nCk{n}{k}=\nCk{n}{n-k}$ の証明
プリントを次のリンクからダウンロードできます。

では,まずは (1) の証明をしてみよう。

右辺を変形して左辺を導きますね!
(右辺)&=\nCk{\color{blue}{n}}{\color{green}{n-k}} \\[4pt]
&=\dfrac{{\color{blue}{n}}!}{({\color{green}{n-k}})!\{{\color{blue}{n}}-({\color{green}{n-k}})\}!} \\[4pt]
&=\dfrac{n!}{(n-k)!k!} \\[4pt]
&=\nCk{n}{k} \\[4pt]
&=(左辺)
\end{align*}

式変形による証明は大丈夫だね。

この等式が当たり前だと思えるように,意味を捉えていつでも使えるようにしよう!
したがって,$\nCk{n}{k}=\nCk{n}{n-k}$ が成り立つ。


意味を考えることで当然だと思えるようになりますね!
$\nCk{n}{k}=\nCk{n-1}{k-1}+\nCk{n-1}{k}$ の証明
プリントを次のリンクからダウンロードできます。

次に (2) の証明をしてみよう。

これも右辺を変形して左辺を導きますね!
(右辺)&=\nCk{\color{blue}{n-1}}{\color{green}{k-1}}
+\nCk{\color{blue}{n-1}}{\color{green}{k}} \\[4pt]
&=\dfrac{({\color{blue}{n-1}})!}{({\color{green}{k-1}})!
\{({\color{blue}{n-1}})-({\color{green}{k-1}})\}!}
+\dfrac{({\color{blue}{n-1}})!}{{\color{green}{k}}!
\{({\color{blue}{n-1}})-{\color{green}{k}}\}!} \\[4pt]
&=\dfrac{(n-1)!}{(k-1)!(n-k)!}+\frac{(n-1)!}{k!(n-k-1)!} \\[4pt]
&=\dfrac{{\color{red}{k}}(n-1)!}{{\color{red}{k}}(k-1)!(n-k)!}
+\dfrac{{\color{red}{(n-k)}}(n-1)!}{k!{\color{red}{(n-k)}}(n-k-1)!} \\[4pt]
&=\dfrac{k\,(n-1)!}{k!(n-k)!}+\frac{(n-k)\,(n-1)!}{k!(n-k)!} \\[4pt]
&=\dfrac{n\,(n-1)!}{k!(n-k)!} \\[4pt]
&=\dfrac{{\color{blue}{n}}!}{{\color{green}{k}}!({\color{blue}{n}}-{\color{green}{k}})!} \\[4pt]
&=\nCk{\color{blue}{n}}{\color{green}{k}} \\[4pt]
&=(左辺)
\end{align*}

いいね!$n(n-1)!=n!$ を利用する通分(赤字部分)の仕方も大丈夫だね。

式変形での証明は結構しんどいです。

そうだね。だからこそ,意味を考えることで,この式をいつでも書けるようにしよう!
(i) 特定の1人を含むとき
(ii) 特定の1人を含まないとき
ここで,特定の1人っていうのは,$n$ 人の中の誰か1人のことで,例えば A 君 とすると,$n$ 人から $k$ 人を選ぶときには,A 君に着目すると A 君が含まれているか含まれていないかのどちらかであるという考え方をしている。
(i) のとき,特定の1人を含むと決めているから,その人を除く $n-1$ 人から残りの $k-1$ 人を選べばよい。よって,その選び方は $\nCk{n-1}{k-1}$ 通り。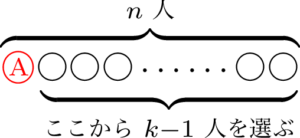
(ii)のとき,特定の1人を含まないと決めているから,その人を除く $n-1$ 人から $k$ 人を選べばよい。よって,その選び方は $\nCk{n-1}{k}$ 通り。
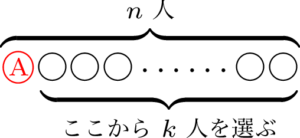
したがって,$\nCk{n}{k}=\nCk{n-1}{k-1}+\nCk{n-1}{k}$ が成り立つ。

なるほど!こう考えればいつでも書けますね!
$k\,\nCk{n}{k}=n\,\nCk{n-1}{k-1}$ の証明
プリントを次のリンクからダウンロードできます。

最後の (3) を証明してみよう。

これは左辺を変形して右辺を導きますね。
(左辺)&=k\,\nCk{\color{blue}{n}}{\color{green}{k}} \\[4pt]&=k\cdot\dfrac{{\color{blue}{n}}!}{{\color{green}{k}}!({\color{blue}{n}}-{\color{green}{k}})!} \\[4pt]&={\color{red}{k}}\cdot\dfrac{n(n-1)!}{{\color{red}{k}}(k-1)!(n-k)!} \\[4pt]&=n\cdot\dfrac{(n-1)!}{(k-1)!(n-k)!} \\[4pt]&=n\cdot\dfrac{({\color{blue}{n-1}})!}{({\color{green}{k-1}})!
\{({\color{blue}{n-1}})-({\color{green}{k-1}})\}!} \\[4pt]&=n\,\nCk{\color{blue}{n-1}}{\color{green}{k-1}} \\[4pt]&=(右辺)
\end{align*}

疲れました・・・

めちゃ頑張ってくれたね!助かるよ。

テスト前にこれを丸暗記してる人もいるけど,結局すぐ忘れるよね?だったら,意味を理解していつでも使いたいときに使えるようにした方が良いよね!
(i) $k$ 人を選んだ後で,その中からリーダー1人を選ぶ。
(ii) $n$ 人からリーダー1人を選んだ後で,残りの $n-1$ 人から リーダー以外の $k-1$ 人を選ぶ。
(i) のとき,$n$ 人から $k$ 人を選ぶ方法が $\nCk{n}{k}$ 通りで,その各々について,その $k$ 人からリーダー1人を選ぶ方法が $k$ 通りある。よって,このときの選ぶ方法の総数は,$k\,\nCk{n}{k}$ 通り。
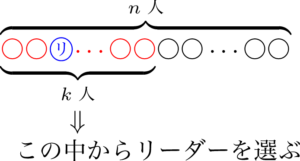
(ii) のとき,$n$ 人からリーダー1人を選ぶ方法が $n$ 通りで,その各々について,リーダー以外の $n-1$ 人から残りの $k-1$ を選ぶ方法が $\nCk{n-1}{k-1}$ 通りある。よって,このときの選ぶ方法の総数は,$n\,\nCk{n-1}{k-1}$ 通り。

したがって,$k\,\nCk{n}{k}=n\,\nCk{n-1}{k-1}$ が成り立つ。

なるほど!これで大丈夫です!
まとめ

意味を考えることで丸暗記しなくて済むね!今日扱った3つの公式をいつでも使えるようにしておこう!
- $\nCk{n}{k}=\nCk{n}{n-k}$
- $\nCk{n}{k}=\nCk{n-1}{k-1}+\nCk{n-1}{k}$
- $k\,\nCk{n}{k}=n\,\nCk{n-1}{k-1}$




















