ここでは,$\sin18\Deg$ の値に関する入試問題を説明します。$\sin18\Deg$ の値を求める問題は,2010年のセンター試験にも出題されていますし,他の様々な大学で出題されているため,試験会場で初めて見たという人はいないでしょう。
角を弧度法(ラジアン)で表せば $\sin18\Deg$ は $\sin\dfrac{\pi}{10}$ となり,どちらも今までに見たことがなく,この記事で初めて見た受験生は,ここでしっかり学習していきましょう。
問題によっては,$\sin18\Deg$ ではなく,$\cos36\Deg$ や $\sin54\Deg$, $\cos72\Deg$ の値を求める問題になっている場合がありますが,基本はすべて同じです。
Contents
- ページ1
- 1 sin18°の値を求める入試問題【2004年 静岡大】
- ページ2
- ページ3
- 1 2006年 岡山県立大
- ページ4
- ページ5
- 1 18の倍数角の正弦・余弦の値に関するまとめ
sin18°の値を求める入試問題【2004年 静岡大】
2004年 静岡大次の問いに答えよ。
(1) $\mathrm{AB=AC}$ である三角形ABCの辺AC上に頂点A, Cと異なる点Dがあり,$\mathrm{AD=DB=BC=1}$ である。このとき,∠Aの大きさを求めよ。
(2) (1)を利用して $\sin18\Deg=\dfrac{\sqrt{5}-1}{4}$ であることを示せ。
(3) $\angle\mathrm{E}=72\Deg$, $\angle\mathrm{F}=\alpha$, $\angle\mathrm{G}=\beta$ である三角形EFGにおいて,$\sin\alpha+\sin\beta$ の最大値を求めよ。
(1) $\mathrm{AB=AC}$ である三角形ABCの辺AC上に頂点A, Cと異なる点Dがあり,$\mathrm{AD=DB=BC=1}$ である。このとき,∠Aの大きさを求めよ。
(2) (1)を利用して $\sin18\Deg=\dfrac{\sqrt{5}-1}{4}$ であることを示せ。
(3) $\angle\mathrm{E}=72\Deg$, $\angle\mathrm{F}=\alpha$, $\angle\mathrm{G}=\beta$ である三角形EFGにおいて,$\sin\alpha+\sin\beta$ の最大値を求めよ。

ヒロ
(1)と(2)は高校入試レベルなので,サクサク解けるようにしよう。

まずは図を描いて状況を把握します。
三角形ABCは二等辺三角形だから,垂直に立っている三角形の方が見た瞬間に,特に意識しなくても二等辺三角形だと分かるように描く。つまり,今回の場合は,BCが底辺になるように二等辺三角形ABCを描く。
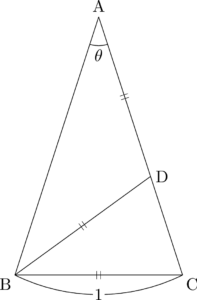
∠Aを求めたいので $\theta$ とおいて,$\theta$ に関する方程式を立てることを考える。$\sin\theta$ などの三角比の値ではなく,$\theta$ を求めないといけないので,三角形の内角の和が $180\Deg$ であることを利用することを考える。
二等辺三角形の性質などを利用して,角の大きさが分かる部分にはどんどん書き込んでいくと次のようになる。
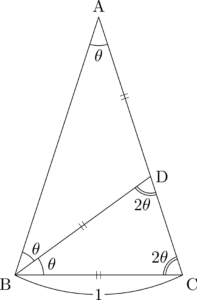
角の大きさを書き込むことで,$\sankaku{ABC}$ の3つの角を $\theta$ で表すことができたから,$\theta$ を求められる。また,副産物として $\sankaku{ABC}$∽$\sankaku{BCD}$ ということも分かった。
【(1)の解答】
$\angle\mathrm{BAC}=\theta$ とおくと,$\mathrm{AD=BD}$ より $\angle\mathrm{ABD}=\theta$ であるから
三角形の内角の和は $180\Deg$ であるから
$\angle\mathrm{BAC}=\theta$ とおくと,$\mathrm{AD=BD}$ より $\angle\mathrm{ABD}=\theta$ であるから
\begin{align*}
\angle\mathrm{BDC}&=\angle\mathrm{BAD}+\angle\mathrm{ABD} \\[4pt]
&=\theta+\theta \\[4pt]
&=2\theta
\end{align*}
さらに,$\mathrm{BD=BC}$ より,$\angle\mathrm{BCD}=2\theta$ である。また,$\mathrm{AB=AC}$ より $\angle\mathrm{ABC}=2\theta$ となる。\angle\mathrm{BDC}&=\angle\mathrm{BAD}+\angle\mathrm{ABD} \\[4pt]
&=\theta+\theta \\[4pt]
&=2\theta
\end{align*}
三角形の内角の和は $180\Deg$ であるから
\begin{align*}
&\theta+2\theta+2\theta=180\Deg \\[4pt]
&5\theta=180\Deg \\[4pt]
&\theta=36\Deg
\end{align*}
&\theta+2\theta+2\theta=180\Deg \\[4pt]
&5\theta=180\Deg \\[4pt]
&\theta=36\Deg
\end{align*}

ヒロ
(2)は(1)をどのように利用するのかがポイントだね。


















