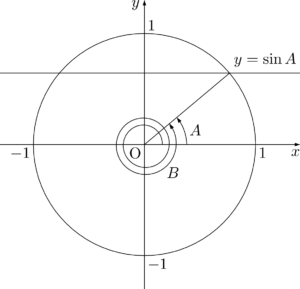
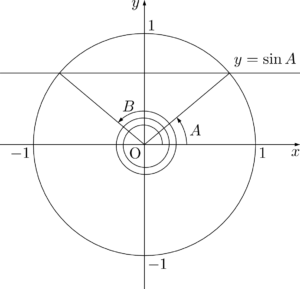
$\sin A=\sin B$ の解き方$\sin A=\sin B$ が成り立つとき,$B$ は整数 $n$ を用いて次のように表すことができる。
\begin{align*}
B=A+2n\pi~~または~~B=\pi-A+2n\pi
\end{align*}
これは単位円で考えると,すぐに納得できるだろう。B=A+2n\pi~~または~~B=\pi-A+2n\pi
\end{align*}



ヒロ
$\cos$ で揃えた場合は,次のようになる。
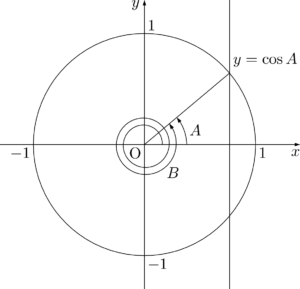
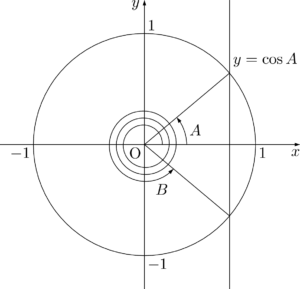
$\cos A=\cos B$ の解き方$\cos A=\cos B$ が成り立つとき,$A$ は整数 $n$ を用いて次のように表すことができる。
\begin{align*}
B=A+2n\pi~~または~~B=-A+2n\pi
\end{align*}
$\sin$ のときと同様に単位円で考えると,簡単に理解できるだろう。B=A+2n\pi~~または~~B=-A+2n\pi
\end{align*}



角 $\theta$ を求めるのだから,$\theta$ に関する方程式を立てることが重要なんですね。これで解いてみます!
【(1)の解答:$\sin$ で揃える】
$\sin2\theta=\cos3\theta$ より
$\sin2\theta=\cos3\theta$ より
\begin{align*}
\sin2\theta=\sin\left(\dfrac{\pi}{2}-3\theta\right)
\end{align*}
$0<\theta<\dfrac{\pi}{2}$ のとき\sin2\theta=\sin\left(\dfrac{\pi}{2}-3\theta\right)
\end{align*}
\begin{align*}
0<2\theta<\pi,~-\pi<\dfrac{\pi}{2}-3\theta<\dfrac{\pi}{2}
\end{align*}
であるから0<2\theta<\pi,~-\pi<\dfrac{\pi}{2}-3\theta<\dfrac{\pi}{2}
\end{align*}
\begin{align*}
&2\theta=\dfrac{\pi}{2}-3\theta \\[4pt]&\theta=\dfrac{\pi}{10}
\end{align*}
&2\theta=\dfrac{\pi}{2}-3\theta \\[4pt]&\theta=\dfrac{\pi}{10}
\end{align*}

簡単ですね。もう1つの解法でも解いておきます!
【(1)の別解:$\cos$ で揃える】
$\sin2\theta=\cos3\theta$ より
$\sin2\theta=\cos3\theta$ より
\begin{align*}
\cos\left(\dfrac{\pi}{2}-2\theta\right)=\cos3\theta
\end{align*}
$0<\theta<\dfrac{\pi}{2}$ のとき\cos\left(\dfrac{\pi}{2}-2\theta\right)=\cos3\theta
\end{align*}
\begin{align*}
-\dfrac{\pi}{2}<\dfrac{\pi}{2}-2\theta<\dfrac{\pi}{2},~0<3\theta<\dfrac{3}{2}\pi
\end{align*}
であるから-\dfrac{\pi}{2}<\dfrac{\pi}{2}-2\theta<\dfrac{\pi}{2},~0<3\theta<\dfrac{3}{2}\pi
\end{align*}
\begin{align*}
&\dfrac{\pi}{2}-2\theta=3\theta \\[4pt]&\theta=\dfrac{\pi}{10}
\end{align*}
&\dfrac{\pi}{2}-2\theta=3\theta \\[4pt]&\theta=\dfrac{\pi}{10}
\end{align*}

ヒロ
完璧だね。最後の(3)を解いていこう。

$\sin\theta$ の値が分かっているからといって,2倍角の公式や3倍角の公式を使って $\sin2\theta$, $\sin3\theta$, $\sin4\theta$ を求めて,さらにそれを掛けて値を求めるとか,どう考えても面倒なので別の方法を考えないとダメですね・・・

ヒロ
ほとんどの人は,解けることに変わりないなら,楽に速く解ける解法を選びたいと思っているはず。

そうですね・・・

ヒロ
入試問題だから,(1)や(2)で分かったことをヒントにするのは当然だね。何が分かったのかしっかり考えよう。

(1)で分かったのは,$\theta=\dfrac{\pi}{10}$ ですけど,もしかして,その前の $5\theta=\dfrac{\pi}{2}$ がヒントになってますか?

ヒロ
何故そう思ったの?

$\theta+4\theta=5\theta$ だし,$2\theta+3\theta=5\theta$ になってて,角の和が $5\theta$ になってるのと関係あるのかなって思いました。

ヒロ
良い着眼点だね!じゃあ,それを利用するとしたら,$5\theta$ が出てくるように式変形すれば良いよね?

なるほど。積和公式を使うとできるかもしれないです。
三角関数の積和公式


















