ここでは数直線上の2点間の距離や平面上の2点間の距離に関する問題について説明します。
大学入試問題で,数直線上の2点間の距離を求める問題が出題されることは,ほとんどないでしょう。
しかし,平面上の2点間の距離に関する問題は出題されることがあります。
基本的な問題ですが,計算間違いをすることなく,確実に得点できるようにしましょう。
数直線上の2点間の距離

ヒロ
非常に基本的ではあるが,まずは数直線上の2点間の距離から説明する。
【数直線上の2点間の距離】
次のように,数直線上に2点A, Bがあるとする。

このときのAB間の長さは,次のように簡単に求めることができるだろう。

このとき,次のように正の部分と負の部分に分けて計算する人がいる。
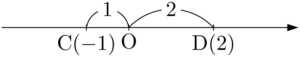
例えば,次のように点の座標が文字の場合に間違った計算をしてしまう可能性がある。

原点を基準に長さを考える人は
したがって,OEの長さは $-a$ としなければならず,
数直線では右に行くほど大きな値になるから,数直線上の2点間の距離を求めるときは,右から左を引けばよく,次のような計算をすると良い。
次のように,数直線上に2点A, Bがあるとする。
このときのAB間の長さは,次のように簡単に求めることができるだろう。
\begin{align*}
\text{AB}=5-2=3
\end{align*}
それでは,次の図の2点CD間の長さを求めてみよう。\text{AB}=5-2=3
\end{align*}
このとき,次のように正の部分と負の部分に分けて計算する人がいる。
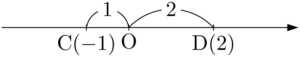
\begin{align*}
\text{CD}&=\text{OC}+\text{OD} \\[4pt]
&=1+2=3
\end{align*}
この考え方でも正しく求められるなら良いが,点の座標が文字で与えられたときに間違えやすいので注意しよう。\text{CD}&=\text{OC}+\text{OD} \\[4pt]
&=1+2=3
\end{align*}
例えば,次のように点の座標が文字の場合に間違った計算をしてしまう可能性がある。
原点を基準に長さを考える人は
\begin{align*}
\text{EF}&=\text{OE}+\text{OF} \\[4pt]
&=a+b
\end{align*}
としてしまうことがある。原点Oとの位置関係から,$a$ は負で $b$ が正であることが分かる。\text{EF}&=\text{OE}+\text{OF} \\[4pt]
&=a+b
\end{align*}
したがって,OEの長さは $-a$ としなければならず,
\begin{align*}
\text{EF}&=\text{OE}+\text{OF} \\[4pt]
&=-a+b
\end{align*}
となる。しかし,丁寧に原点からの距離を分けて計算するから,このような間違いをしてしまうのである。\text{EF}&=\text{OE}+\text{OF} \\[4pt]
&=-a+b
\end{align*}
数直線では右に行くほど大きな値になるから,数直線上の2点間の距離を求めるときは,右から左を引けばよく,次のような計算をすると良い。
\begin{align*}
\text{EF}=b-a
\end{align*}
ただし,これは2点E,Fの位置関係(どちらが右側にあるか)が分かっているから引く順番が分かるのであり,2点の位置関係が分からない問題も多い。そのような場合は,「計算結果が正になるようにする」ことを考えると,とりあえず差をとって絶対値を取れば良いことが分かるだろう。つまり,$a$ と $b$ の大小関係が分からない場合は\text{EF}=b-a
\end{align*}
\begin{align*}
\text{EF}=\abs{a-b}
\end{align*}
としておけば良いのである。もちろん $\abs{b-a}$ でも構わない。\text{EF}=\abs{a-b}
\end{align*}

ヒロ
ということで,話をまとめると次のようになる。
数直線上の2点間の距離数直線上の2点A$(a)$, B$(b)$について,AB間の距離は
\begin{align*}
\text{AB}=\abs{a-b}
\end{align*}
と表せる。\text{AB}=\abs{a-b}
\end{align*}
平面上の2点間の距離

ヒロ
それでは,次に平面上の2点間の距離を考える。
【平面上の2点間の距離】
平面上の2点A$(a,~b)$,B$(c,~d)$について,AB間の距離を考える。例えば下図のようになっているとする。
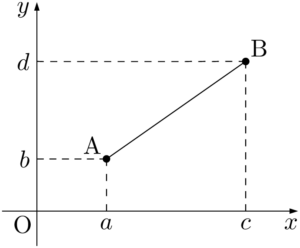
ABを斜辺とする直角三角形ABCを考える。
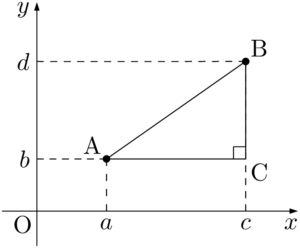
直角三角形ABCに対して,三平方の定理を用いると
いまは2点A,Bを第1象限にとったが,どこにあっても同じ計算でABの長さを求めることができる。
平面上の2点A$(a,~b)$,B$(c,~d)$について,AB間の距離を考える。例えば下図のようになっているとする。

ABを斜辺とする直角三角形ABCを考える。

直角三角形ABCに対して,三平方の定理を用いると
\begin{align*}
\text{AB}&=\sqrt{\text{AC}^2+\text{BC}^2} \\[4pt]
&=\sqrt{(c-a)^2+(d-b)^2}
\end{align*}
となる。\text{AB}&=\sqrt{\text{AC}^2+\text{BC}^2} \\[4pt]
&=\sqrt{(c-a)^2+(d-b)^2}
\end{align*}
いまは2点A,Bを第1象限にとったが,どこにあっても同じ計算でABの長さを求めることができる。
平面上の2点間の距離平面上の2点A$(a,~b)$,B$(c,~d)$について,AB間の距離は
\begin{align*}
\text{AB}=\sqrt{(a-c)^2+(b-d)^2}
\end{align*}
と表せる。$a$ と $c$ の引く順序については $a-c$ と $c-a$ のどちらでも構わない。$b$ と $d$ についても同様である。\text{AB}=\sqrt{(a-c)^2+(b-d)^2}
\end{align*}
点の座標を求める問題【湘南工科大】
2012年 湘南工科大・改2点A$(1,~10)$, B$(2,~11)$ から等距離にある $x$ 軸上の点をCとする。このとき,Cの $x$ 座標を求めよ。
【考え方と解答】
点Cは $x$ 軸上の点だから $y$ 座標は0である。したがって,C$(c,~0)$ とおくことができる。未知数は $c$ 1つだけだから,与えられた条件から $c$ に関する方程式を立てることを考えると,$\text{AC}=\text{BC}$ を $c$ で表せば良いことが分かるだろう。そのまま立式すると根号が邪魔だから,両辺を2乗した $\text{AC}^2=\text{BC}^2$ で考える。
点Cは $x$ 軸上の点だから $y$ 座標は0である。したがって,C$(c,~0)$ とおくことができる。未知数は $c$ 1つだけだから,与えられた条件から $c$ に関する方程式を立てることを考えると,$\text{AC}=\text{BC}$ を $c$ で表せば良いことが分かるだろう。そのまま立式すると根号が邪魔だから,両辺を2乗した $\text{AC}^2=\text{BC}^2$ で考える。
\begin{align*}
&(c-1)^2+10^2=(c-2)^2+11^2 \\[4pt]
&(c-1)^2-(c-2)^2=11^2-10^2
\end{align*}
ここでする計算は「2乗の差」であるから,因数分解を利用して計算しよう。&(c-1)^2+10^2=(c-2)^2+11^2 \\[4pt]
&(c-1)^2-(c-2)^2=11^2-10^2
\end{align*}
\begin{align*}
&\{(c-1)+(c-2)\}\{(c-1)-(c-2)\}=(11+10)(11-10) \\[4pt]
&2c-3=21 \\[4pt]
&c=12
\end{align*}
よって,求める点Cの $x$ 座標は12である。&\{(c-1)+(c-2)\}\{(c-1)-(c-2)\}=(11+10)(11-10) \\[4pt]
&2c-3=21 \\[4pt]
&c=12
\end{align*}

ヒロ
「2乗の差」の計算では,2乗の中身の差が1のときは特に楽に計算できるので,計算するのが嫌な人・苦手な人ほど利用して欲しい。
点の座標を求める問題【小樽商科大】
2019年 小樽商科大$x$ と $y$ は実数で $y>0$ とする。座標平面に点O$(0,~0)$,点A$(6,~0)$ および点B $(x,~y)$ を取る。辺OBの長さが5,辺ABの長さが9のとき,$(x,~y)=\myhako$ である。
【考え方と解答】
与えられた条件を $x,~y$ を用いて表して,方程式を立てよう。
辺OBの長さが5であるから
よって,$(x,~y)=\left(-\dfrac{5}{3},~\dfrac{10\sqrt{2}}{3}\right)$
与えられた条件を $x,~y$ を用いて表して,方程式を立てよう。
辺OBの長さが5であるから
\begin{align*}
&\text{OB}^2=25 \\[4pt]&x^2+y^2=25~\cdots\cdots①
\end{align*}
辺ABの長さが9であるから&\text{OB}^2=25 \\[4pt]&x^2+y^2=25~\cdots\cdots①
\end{align*}
\begin{align*}
&\text{AB}^2=81 \\[4pt]&(x-6)^2+y^2=81~\cdots\cdots②
\end{align*}
$①-②$ より&\text{AB}^2=81 \\[4pt]&(x-6)^2+y^2=81~\cdots\cdots②
\end{align*}
\begin{align*}
&x^2-(x-6)^2=25-81 \\[4pt]&6(2x-6)=-56 \\[4pt]&x=-\dfrac{5}{3}
\end{align*}
このとき①より&x^2-(x-6)^2=25-81 \\[4pt]&6(2x-6)=-56 \\[4pt]&x=-\dfrac{5}{3}
\end{align*}
\begin{align*}
y^2=25-\dfrac{25}{9}=\dfrac{25\Cdot8}{9}
\end{align*}
$y>0$ より $y=\dfrac{10\sqrt{2}}{3}$y^2=25-\dfrac{25}{9}=\dfrac{25\Cdot8}{9}
\end{align*}
よって,$(x,~y)=\left(-\dfrac{5}{3},~\dfrac{10\sqrt{2}}{3}\right)$




















