具体的な円錐面の方程式を考え,その円錐面を様々な平面で切断したときに現れる二次曲線(放物線・楕円・双曲線)の方程式を求めることで理解を深めましょう。
また,離心率の定義や離心率の値によって,どのような二次曲線になるかを知っておくことで,入試では有利になります。
Contents
二次曲線は円錐面を切断することで現れる【円錐曲線】

ヒロ
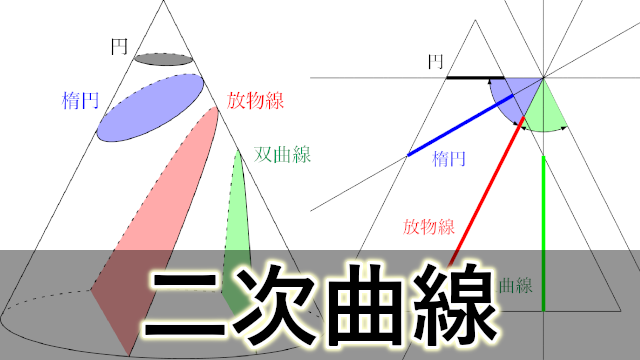
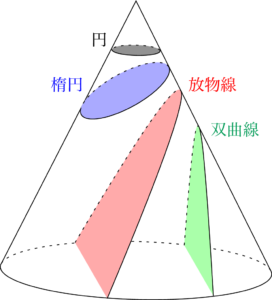
円錐面を平面で切断したときの様子は次のようになる。

ヒロ
円錐と平面の角度によって現れる曲線が決まり,円・楕円・放物線・双曲線が現れる。円錐を切断したときに現れる曲線だから,円錐曲線とも呼ばれる。
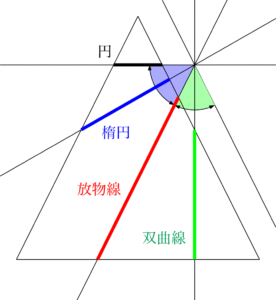
【円錐面の平面による断面図】



ヒロ
円錐の中心軸に垂直な平面で切った断面は円になる。

ヒロ
母線と平行になるまでの青色の角度の範囲なら楕円,母線と平行になったときが放物線,緑色の角度の範囲なら双曲線になる。