ここでは同じものを含む順列について説明します。
同じものを含むものを1列に並べるとき,同じもの同士の場所を入れ替えても同じ順列とみなします。
どのようにして同じものを含む順列の総数を求めるのか,正しい考え方を身に付けて得点力をアップさせましょう。
同じものを含む順列の総数を求める問題

ヒロ
例えば次の問題を考えてみよう。
問題a, a, a, b, b, cの6個の文字すべてを1列に並べる方法は何通りあるか。
【考え方と解答】
6個の文字を並べる場所を1~6とすると,次の3つの手順で6個の文字を1列に並べることができる。
① 1~6の6か所から3か所を選んでaを置く。
② 1~6のうち,aを置いた3か所を除いた残り3か所から2か所を選んでbを置く。
③ 最後に残った場所にcを置く。
①の方法は $\nCk{6}{3}$ 通り。②の方法は $\nCk{3}{2}$ 通り。③の方法は1通り。よって
6個の文字を並べる場所を1~6とすると,次の3つの手順で6個の文字を1列に並べることができる。
① 1~6の6か所から3か所を選んでaを置く。
② 1~6のうち,aを置いた3か所を除いた残り3か所から2か所を選んでbを置く。
③ 最後に残った場所にcを置く。
①の方法は $\nCk{6}{3}$ 通り。②の方法は $\nCk{3}{2}$ 通り。③の方法は1通り。よって
\begin{align*}
\nCk{6}{3}\times\nCk{3}{2}\times1&=20\times3=60~通り
\end{align*}
\nCk{6}{3}\times\nCk{3}{2}\times1&=20\times3=60~通り
\end{align*}

ヒロ
個数が多い文字から考えると $\nCk{n}{r}$ の $r$ が大きくなって計算が面倒なので,個数が少ない文字から考えた方が良い。
【別解】
6個の文字を並べる場所を1~6とすると,次の3つの手順で6個の文字を1列に並べることができる。
① 1~6から1か所を選んでcを置く。
② cを置いた場所以外の5か所から2か所を選んでbを置く。
③ 残った3か所にaを置く。
①の方法は6通り。②の方法は $\nCk{5}{2}$ 通り。③の方法は1通り。よって
6個の文字を並べる場所を1~6とすると,次の3つの手順で6個の文字を1列に並べることができる。
① 1~6から1か所を選んでcを置く。
② cを置いた場所以外の5か所から2か所を選んでbを置く。
③ 残った3か所にaを置く。
①の方法は6通り。②の方法は $\nCk{5}{2}$ 通り。③の方法は1通り。よって
\begin{align*}
6\times\nCk{5}{2}\times1=6\times10=60~通り
\end{align*}
6\times\nCk{5}{2}\times1=6\times10=60~通り
\end{align*}

ヒロ
円順列のときのように重複も含めて数えてから調整したい人は次のように考えよう。
【別の考え方と解答】
同じ文字が複数あるけど,3つのaを a$_1$, a$_2$, a$_3$, b$_1$, b$_2$ と区別すると,異なる6文字を1列に並べることになる。このときの並べ方は
a$_1$a$_2$a$_3$b$_1$b$_2$
a$_1$a$_3$a$_2$b$_1$b$_2$
a$_2$a$_1$a$_3$b$_1$b$_2$
a$_2$a$_3$a$_1$b$_1$b$_2$
a$_3$a$_1$a$_2$b$_1$b$_2$
a$_3$a$_2$a$_1$b$_1$b$_2$
1つの並べ方に対して,aを区別すると6通り現れるものを1通りとみなすから「6で割る」ことになる。
また2つあるbについても同じことが言える。異なる2つのものを並べる方法は $2!=2$ 通りあるから「2で割る」ことで重複をなくすことができる。
よって,求める場合の数は
同じ文字が複数あるけど,3つのaを a$_1$, a$_2$, a$_3$, b$_1$, b$_2$ と区別すると,異なる6文字を1列に並べることになる。このときの並べ方は
\begin{align*}
6!=720~通り
\end{align*}
となる。しかし実際には a$_1$, a$_2$, a$_3$ の3文字はaだから,この3文字を好きなように入れ替えても同じ並べ方となる。異なる3文字の並べ方は $3!=6$ 通りある。例えば「aaabbc」という文字列で3つのaをすべて区別すると次の6通りがある。6!=720~通り
\end{align*}
a$_1$a$_2$a$_3$b$_1$b$_2$
a$_1$a$_3$a$_2$b$_1$b$_2$
a$_2$a$_1$a$_3$b$_1$b$_2$
a$_2$a$_3$a$_1$b$_1$b$_2$
a$_3$a$_1$a$_2$b$_1$b$_2$
a$_3$a$_2$a$_1$b$_1$b$_2$
1つの並べ方に対して,aを区別すると6通り現れるものを1通りとみなすから「6で割る」ことになる。
また2つあるbについても同じことが言える。異なる2つのものを並べる方法は $2!=2$ 通りあるから「2で割る」ことで重複をなくすことができる。
よって,求める場合の数は
\begin{align*}
\dfrac{6!}{3!2!}=\dfrac{720}{6\Cdot2}=60~通り
\end{align*}
\dfrac{6!}{3!2!}=\dfrac{720}{6\Cdot2}=60~通り
\end{align*}
同じものを含む順列の総数を求める問題2

ヒロ
簡単な入試問題を解いてみよう。
2019年 神奈川大KANAGAWAの8文字をすべて使って1列に並べる並べ方は,全部で $\myhako$ 通りある。

ヒロ
文字を並べるときは同じ文字があるかどうか確認しよう。
【考え方と解答】
文字の種類と個数を調べると,次のようになっている。
K, N, G, W・・・1個ずつ,A・・・4個
K, N, G, W, Aの順に置く場所を決めると,並べ方は
文字の種類と個数を調べると,次のようになっている。
K, N, G, W・・・1個ずつ,A・・・4個
K, N, G, W, Aの順に置く場所を決めると,並べ方は
\begin{align*}
8\Cdota7\Cdota6\Cdota5=1680~通り
\end{align*}
8\Cdota7\Cdota6\Cdota5=1680~通り
\end{align*}

ヒロ
重複を含めて数える場合は次のようになる。
【別解】
すべて異なるとすると $8!$ 通りあるが,Aが4個あるため1つの並べ方に対して $4!$ 通りが重複するから
すべて異なるとすると $8!$ 通りあるが,Aが4個あるため1つの並べ方に対して $4!$ 通りが重複するから
\begin{align*}
\dfrac{8!}{4!}=1680~通り
\end{align*}
\dfrac{8!}{4!}=1680~通り
\end{align*}
同じものを含む順列の総数を求める問題3

ヒロ
「隣り合う」「隣り合わない」などの条件が付く問題もある。
東邦大A, A, A, B, B, C, Dの7文字を1列に並べるとき,次の問いに答えよ。
(1) Aが隣り合わない並べ方は何通りあるか。
(2) (1)の並べ方のうち,BABという並びを含むものは何通りあるか。
(3) Aは隣り合わず,Bも隣り合わない並べ方は何通りあるか。
(1) Aが隣り合わない並べ方は何通りあるか。
(2) (1)の並べ方のうち,BABという並びを含むものは何通りあるか。
(3) Aは隣り合わず,Bも隣り合わない並べ方は何通りあるか。

ヒロ
「隣り合う」「隣り合わない」の条件が付いたときの考え方を忘れている人は次の記事を読んで復習しよう。
【(1)の考え方と解答】
次の手順で条件を満たすように並べることができる。
① B, B, C, Dの4文字を並べる。
② ①で並べた4文字の間と両端の5か所から3か所を選んでAを並べる。
①の方法は $\dfrac{4!}{2!}$ 通りあり,②の方法は $\nCk{5}{3}$ 通りあるから,
次の手順で条件を満たすように並べることができる。
① B, B, C, Dの4文字を並べる。
② ①で並べた4文字の間と両端の5か所から3か所を選んでAを並べる。
①の方法は $\dfrac{4!}{2!}$ 通りあり,②の方法は $\nCk{5}{3}$ 通りあるから,
\begin{align*}
\dfrac{4!}{2!}\times\nCk{5}{3}=12\times10=120~通り
\end{align*}
\dfrac{4!}{2!}\times\nCk{5}{3}=12\times10=120~通り
\end{align*}
(2) (1)の並べ方のうち,BABという並びを含むものは何通りあるか。
【(2)の考え方と解答】
「BABという並び」を考えるときはBABを1つのカタマリにして考えれば良いね。つまり次の手順で考える。
① BAB, C, Dの3つを並べる。
② ①で並べたものの間と両端の4か所から2か所を選んでAを並べる。
①の方法は $3!$ 通りあり,②の方法は $\nCk{4}{2}$ 通りあるから
「BABという並び」を考えるときはBABを1つのカタマリにして考えれば良いね。つまり次の手順で考える。
① BAB, C, Dの3つを並べる。
② ①で並べたものの間と両端の4か所から2か所を選んでAを並べる。
①の方法は $3!$ 通りあり,②の方法は $\nCk{4}{2}$ 通りあるから
\begin{align*}
3!\times\nCk{4}{2}=6\times6=36~通り
\end{align*}
3!\times\nCk{4}{2}=6\times6=36~通り
\end{align*}
(3) Aは隣り合わず,Bも隣り合わない並べ方は何通りあるか。
【(3)の考え方と解答】
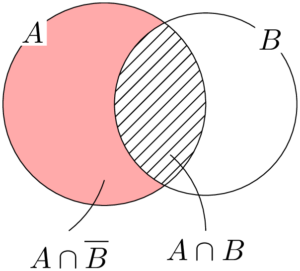
隣り合わないものが複数ある問題では,数え方を工夫しよう。例えば「Aが隣り合わない」「Bが隣り合わない」という事象をそれぞれ $A,~B$ とすると,求める場合の数は $n(A\cap B)$ と表すことができる。ここで次のようなベン図を考える。
ベン図より,次の等式が成り立つ。
次の2つの手順を考えて $n(A\cap\overline{B})$ を求めよう。
① BB, C, Dの3つを並べる。
② ①で並べた3つのものの間と両端の4か所から3か所を選んでAを並べる。
①の方法は $3!$ 通りあり,②の方法は $\nCk{4}{3}$ 通りあるから,
隣り合わないものが複数ある問題では,数え方を工夫しよう。例えば「Aが隣り合わない」「Bが隣り合わない」という事象をそれぞれ $A,~B$ とすると,求める場合の数は $n(A\cap B)$ と表すことができる。ここで次のようなベン図を考える。

ベン図より,次の等式が成り立つ。
\begin{align*}
n(A\cap B)=n(A)-n(A\cap\overline{B})
\end{align*}
$n(A)$ は「Aが隣り合わない並べ方の総数」となり,すでに(1)で求めている。また,$n(A\cap\overline{B})$ は「Aが隣り合わず,Bは隣り合う並べ方の総数」となり,2つのBを1つのカタマリと見ることで数えることができる。n(A\cap B)=n(A)-n(A\cap\overline{B})
\end{align*}
次の2つの手順を考えて $n(A\cap\overline{B})$ を求めよう。
① BB, C, Dの3つを並べる。
② ①で並べた3つのものの間と両端の4か所から3か所を選んでAを並べる。
①の方法は $3!$ 通りあり,②の方法は $\nCk{4}{3}$ 通りあるから,
\begin{align*}
3!\times\nCk{4}{3}=6\times4=24~通り
\end{align*}
したがって,求める場合の数は3!\times\nCk{4}{3}=6\times4=24~通り
\end{align*}
\begin{align*}
120-24=96~通り
\end{align*}
120-24=96~通り
\end{align*}





















