Contents
円錐面の方程式の導出

ヒロ
ここで,次の問題を考えて,円錐面の方程式を導出しよう。
例題1$z$ 軸を円錐の中心軸とする直円錐を考える。頂点の座標が $(0,~0,~k)$ であり,$xy$ 平面との交わりが半径 $r$ の円となるような円錐面の方程式を求めよ。

ヒロ
点が円錐面上にある条件を考えよう。
円錐の頂点をAとし,円錐面上の点を $\mathrm{P}(x,~y,~z)$ とする。また,図のように,APと $z$ 軸のなす角を $\theta$ とし,$\vec{d}=(0,~0,~-1)$ とする。
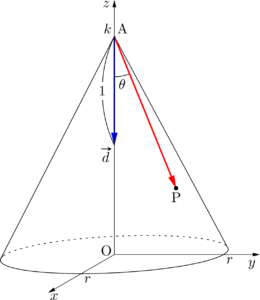
点Pが円錐面上にあるための条件は,$\Vec{AP}$ と $\vec{d}$ のなす角が $\theta$ であることだから,

点Pが円錐面上にあるための条件は,$\Vec{AP}$ と $\vec{d}$ のなす角が $\theta$ であることだから,
\begin{align*}
&\Vec{AP}\Cdota\vec{d}=\abs{\Vec{AP}}\abs{\vec{d}}\cos\theta \\[4pt]
&-(z-k)=\sqrt{x^2+y^2+(z-k)^2}\cos\theta
\end{align*}
$z\leqq k$ より,$-(z-k)\geqq0$ である。また $\cos\theta>0$ より,両辺は0以上であるから,両辺を2乗して&\Vec{AP}\Cdota\vec{d}=\abs{\Vec{AP}}\abs{\vec{d}}\cos\theta \\[4pt]
&-(z-k)=\sqrt{x^2+y^2+(z-k)^2}\cos\theta
\end{align*}
\begin{align*}
&(z-k)^2=(x^2+y^2+(z-k)^2)\cos^2\theta
\end{align*}
$\cos\theta=\dfrac{k}{\sqrt{k^2+r^2}}$ より&(z-k)^2=(x^2+y^2+(z-k)^2)\cos^2\theta
\end{align*}
\begin{align*}
&(z-k)^2=(x^2+y^2+z^2)\Cdota\dfrac{k^2}{k^2+r^2} \\[4pt]
&(k^2+r^2)(z-k)^2=k^2(x^2+y^2+(z-k)^2) \\[4pt]
&k^2(x^2+y^2)=r^2(z-k)^2
\end{align*}
&(z-k)^2=(x^2+y^2+z^2)\Cdota\dfrac{k^2}{k^2+r^2} \\[4pt]
&(k^2+r^2)(z-k)^2=k^2(x^2+y^2+(z-k)^2) \\[4pt]
&k^2(x^2+y^2)=r^2(z-k)^2
\end{align*}

ヒロ
これで円錐面の方程式の導出ができたね。
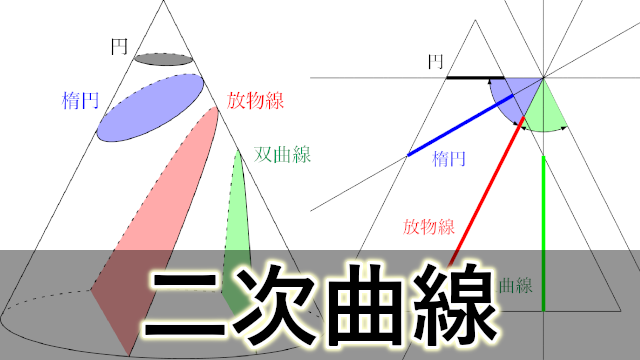
二次曲線の方程式の求め方【円錐面を切断】

ヒロ
具体的な円錐面を平面で切断して,交線の方程式を求めてみよう。
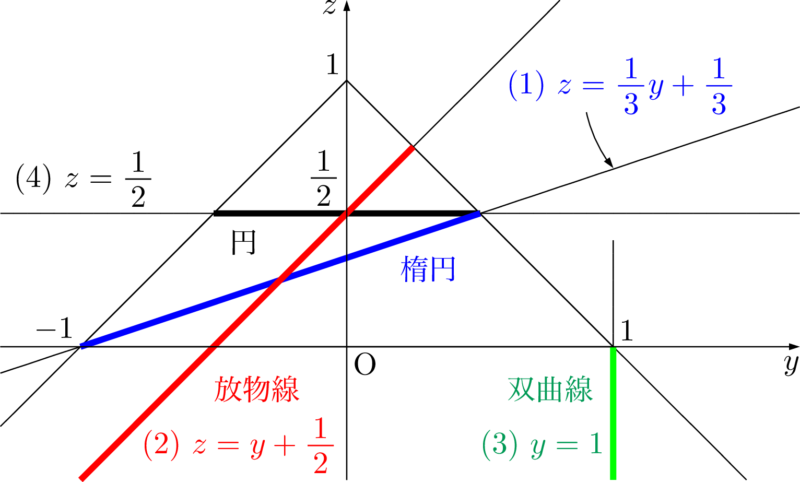
例題2円錐面:$x^2+y^2=(z-1)^2$ を次の平面で切断したときに現れる曲線を求めよ。
(1) $z=\dfrac{1}{3}y+\dfrac{1}{3}$
(2) $z=y+\dfrac{1}{2}$
(3) $y=1$
(4) $z=\dfrac{1}{2}$
(1) $z=\dfrac{1}{3}y+\dfrac{1}{3}$
(2) $z=y+\dfrac{1}{2}$
(3) $y=1$
(4) $z=\dfrac{1}{2}$

ヒロ
ただの連立方程式だと思って手を動かして計算してみよう。
【(1)の解答】
$x^2+y^2=(z-1)^2~\cdots\cdots①$ に $z=\dfrac{1}{3}y+\dfrac{1}{3}$ を代入すると
$x^2+y^2=(z-1)^2~\cdots\cdots①$ に $z=\dfrac{1}{3}y+\dfrac{1}{3}$ を代入すると
\begin{align*}
&x^2+y^2=\left(\dfrac{1}{3}y-\dfrac{2}{3}\right)^2 \\[4pt]
&x^2+\dfrac{8}{9}y^2+\dfrac{4}{9}y=\dfrac{4}{9} \\[4pt]
&x^2+\dfrac{8}{9}\left(y+\dfrac{1}{4}\right)^2=\dfrac{1}{2} \\[4pt]
&\dfrac{x^2}{\dfrac{1}{2}}+\dfrac{\left(y+\dfrac{1}{4}\right)^2}{\dfrac{9}{16}}=1
\end{align*}
これは楕円である。&x^2+y^2=\left(\dfrac{1}{3}y-\dfrac{2}{3}\right)^2 \\[4pt]
&x^2+\dfrac{8}{9}y^2+\dfrac{4}{9}y=\dfrac{4}{9} \\[4pt]
&x^2+\dfrac{8}{9}\left(y+\dfrac{1}{4}\right)^2=\dfrac{1}{2} \\[4pt]
&\dfrac{x^2}{\dfrac{1}{2}}+\dfrac{\left(y+\dfrac{1}{4}\right)^2}{\dfrac{9}{16}}=1
\end{align*}

ヒロ
(1)と同じように解こう。
【(2)の解答】
①に $z=y+\dfrac{1}{2}$ を代入すると
①に $z=y+\dfrac{1}{2}$ を代入すると
\begin{align*}
&x^2+y^2=\left(y-\dfrac{1}{2}\right)^2 \\[4pt]
&x^2=-y+\dfrac{1}{4} \\[4pt]
&y=-x^2+\dfrac{1}{4}
\end{align*}
これは放物線である。&x^2+y^2=\left(y-\dfrac{1}{2}\right)^2 \\[4pt]
&x^2=-y+\dfrac{1}{4} \\[4pt]
&y=-x^2+\dfrac{1}{4}
\end{align*}

ヒロ
最後の(3)を解こう。
【(3)の解答】
①に $y=1$ を代入すると
①に $y=1$ を代入すると
\begin{align*}
&x^2+1=(z-1)^2 \\[4pt]
&x^2-(z-1)^2=-1
\end{align*}
これは双曲線である。&x^2+1=(z-1)^2 \\[4pt]
&x^2-(z-1)^2=-1
\end{align*}

ヒロ
(4)は $xy$ 平面に平行な平面だから,断面は円になるはず。
【(4)の解答】
①に $z=\dfrac{1}{2}$ を代入すると
①に $z=\dfrac{1}{2}$ を代入すると
\begin{align*}
&x^2+y^2=\left(-\dfrac{1}{2}\right)^2 \\[4pt]
&x^2+y^2=\dfrac{1}{4}
\end{align*}
これは円である。&x^2+y^2=\left(-\dfrac{1}{2}\right)^2 \\[4pt]
&x^2+y^2=\dfrac{1}{4}
\end{align*}

ヒロ
$x$ 軸がこちらに向かう方向から見た図で確認しておこう。
【円錐を真横から見た図】