平均値の定理を利用して不等式を証明するのって難しいですよね。しかし,それは平均値の定理の利用方法を勘違いしているのが原因です。
おそらくほとんどの人は,平均値の定理を等式と認識していて,等式を不等式の証明に利用すると考えているから,平均値の定理を利用した不等式の証明問題が苦手になるのです。
正しい考え方と平均値の定理の利用方法を身に付けて,この手の問題を苦手から得意に変えましょう。2013年の名古屋大で出題された入試問題を用いて説明します。
\dfrac{100}{x+1}<f(x+1)-f(x)<\dfrac{100}{x}
\end{align*}
平均値の定理とは

平均値の定理を利用すると思うんですけど,どうすれば良いのかさっぱり分かりません。

まず,この不等式を見たときに「$f(x+1)-f(x)$」があることに着目しよう。不等式の証明において,$f(b)-f(a)$ の形を見たときは平均値の定理を利用することを意識しよう!
関数 $f(x)$ が $a\leqq x\leqq b$ で連続で,$a<x<b$ で微分可能なとき,
$\quad\displaystyle\frac{f(b)-f(a)}{b-a}=f'(c)$
となる $c~(a<c<b)$ が存在する。
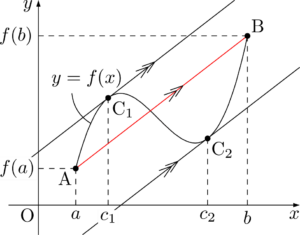
上図では,曲線 $y=f(x)$ 上の点の接線の傾きが線分ABの傾きと等しくなる点が${\mathrm C}_1,{\mathrm C}_2$ の2点ある。
平均値の定理を利用して不等式の証明をする方法

平均値の定理を利用するって言われても,証明したいのは不等式なのに,平均値の定理って等式じゃないですか。どうやって利用するんですか?

そう,多くの人がそこに悩む。最大のポイントは平均値の定理に出てくる $c$ だよ。

前に,不等式の証明方法として,「既に分かっている不等式を利用する」という考え方を教えたよね?

はい!覚えてます!

平均値の定理を利用した不等式の証明では,平均値の定理の等式を条件とする条件つき不等式の証明と捉えよう。つまり,サブのような不等式である $a<c<b$ を変形していく過程で,平均値の定理の等式をうまく使って証明したい不等式を導くんだ。

なるほど!今回は $f(x)$ が与えられているから,その部分は考えなくて済みますね!

その点は楽だね。ということで,解答を書いていこう。
&\frac{f(x+1)-f(x)}{(x+1)-x}=f'(c) \\[4pt]
&f(x+1)-f(x)=\frac{100}{c}\ \cdots ①
\end{align*}

ここから ② を証明したい不等式に近づくように変形していくよ。
&\frac{1}{x+1}<\frac{1}{c}<\frac{1}{x} \\[4pt]
&\frac{100}{x+1}<\frac{100}{c}<\frac{100}{x}\ \cdots ③
\end{align*}

これで両側が全く同じ式になったから,真ん中の式を①を使って変えるだけ。
\displaystyle \frac{100}{x+1}<f(x+1)-f(x)<\frac{100}{x}
\end{align*}

めちゃくちゃ簡単ですね!
練習問題を解いて慣れよう!

じゃあ,もう次の練習問題をやってみよう。
a-b<b\log b-a\log a<b-a
\end{align*}

これは自分で $f(x)$ を決めないといけないんですね?

そうだね。$f(x)$ をどう決めれば良いか分かるかな?

真ん中の $b\log b-a\log a$ を $f(b)-f(a)$ と見れば良いんですか?

いいね!

ということは,$f(x)=x\log x$ とするんですね!

そうだね。じゃあ解答を進めてみよう。
&\frac{f(b)-f(a)}{b-a}=f'(c) \\
&\frac{f(b)-f(a)}{b-a}=\log c+1\ \cdots ①
\end{align*}
$\displaystyle b>a>\frac{1}{e^2}>0$であるから,②より
&\log a<\log c<\log b \\[4pt]&\log a+1<\log c+1<\log b+1\ \cdots ③
\end{align*}
\log a+1<\frac{f(b)-f(a)}{b-a}<\log b+1\ \cdots ④
\end{align*}

ここまでは来ましたけど,辺々に $b-a$ を掛けても証明したい不等式になりません。

ほぼ完成というところまでは来たね。これで証明できないから間違ってるなんてことは思わないように。

$A<B<C$ を証明しようとして,$D<B<E$ が証明できたんだ。このとき,あとは何を証明すれば良いかを考えよう!

なるほど!それなら,$A<D$ と $E<C$ を証明すれば良いんですね!

完璧だね!大小関係を勘違いしてしまうことがあるから注意しよう!

その考え方を今回の問題に適用するとどうなるかな?

$-1<\log a+1$ と $\log b+1<1$ を証明すれば良いんですね!

そう!あとはそれをどうやって証明するか・・・だね。

$a$ と $b$ の範囲が関係するんですか?

使っていない条件に着目するのがいいね!
&\log\frac{1}{e^2}<\log a \\[4pt]&-2<\log a \\[4pt]&-1<\log a+1\ \cdots ⑤
\end{align*}
&\log b<0 \\[4pt]&\log b+1<1\ \cdots ⑥
\end{align*}
-1<\frac{f(b)-f(a)}{b-a}<1
\end{align*}
a-b<b\log b-a\log a<b-a
\end{align*}

出来ました!

いいね!これでこの形式なら大抵の問題は解けるんじゃないかな。

色んな問題を解いて練習しておきます。
まとめ

今回扱った平均値の定理を利用した不等式の証明問題は,出題頻度としてはそれほど高くないけど,出来る・出来ないをはっきり分ける問題だね。しっかりポイントを押さえておこう!
- 平均値の定理の $c$ の範囲を表す不等式をメインと考える。
- 平均値の定理の等式は不等式を変形する際の条件と考える。
- 一発で導きたい不等式にならなくても諦めず,二段階になってる問題なんだと前向きに考える。
- 行き詰ったら,まだ使っていない条件に着目する。





















