離心率と二次曲線に関連する入試問題【札幌医科大】

Contents

二次曲線の極方程式と離心率・半直弦

ヒロ

一般に，二次曲線と呼ばれる放物線・楕円・双曲線の極方程式は $r=\dfrac{l}{1-\varepsilon\cos\theta}$ $(l\geqq0,~\varepsilon>0)$ と表すことができる。ここで，$\varepsilon,~l$ はそれぞれ離心率，半直弦と呼ばれる定数である。

ヒロ

導出できない人は個別記事へ飛んで確認しておこう。

二次曲線の離心率に関する入試問題【2018年札幌医科大】

2018年札幌医科大$a>0$ とし，点 $\mathrm{P}(x,~y)$ は，$y$ 軸からの距離 $d_1$ と点 $(2,~0)$ からの距離 $d_2$ が $ad_1=d_2$ をみたすものとする。$a$ が次の値のとき，点 $\mathrm{P}(x,~y)$ の軌跡を求めよ。
(1) $a=\dfrac{1}{2}$
(2) $a=1$
(3) $a=2$

ヒロ

この問題を読んだ直後に，$a$ が離心率であることが分かるようにしておこう。

ヒロ

(1)は楕円になるはず。実際に計算していこう。

【(1)の解答】
$\dfrac{1}{2}d_1=d_2$ より $\dfrac{1}{4}{d_1}^2={d_2}^2$ が成り立つから

\begin{align*}
&\dfrac{1}{4}x^2=(x-2)^2+y^2 \\[4pt]
&\dfrac{3}{4}x^2-4x+y^2=-4 \\[4pt]
&\dfrac{3}{4}\left(x-\dfrac{8}{3}\right)^2+y^2=\dfrac{4}{3} \\[4pt]
&\dfrac{9}{16}\left(x-\dfrac{8}{3}\right)^2+\dfrac{3}{4}y^2=1
\end{align*}

よって，点Pの軌跡は楕円 $\dfrac{9}{16}\left(x-\dfrac{8}{3}\right)^2+\dfrac{3}{4}y^2=1$

ヒロ

(2)は放物線になるはず。

【(2)の解答】
$d_1=d_2$ より ${d_1}^2={d_2}^2$ が成り立つから

\begin{align*}
&x^2=(x-2)^2+y^2 \\[4pt]
&0=-4x+4+y^2 \\[4pt]
&x=\dfrac{1}{4}y^2+1
\end{align*}

よって，点Pの軌跡は放物線 $x=\dfrac{1}{4}y^2+1$

ヒロ

(3)は双曲線になるはず。

【(3)の解答】
$2d_1=d_2$ より $4{d_1}^2={d_2}^2$ が成り立つから

\begin{align*}
&4x^2=(x-2)^2+y^2 \\[4pt]
&3x^2=-4x+4+y^2 \\[4pt]
&3\left(x+\dfrac{2}{3}\right)^2-y^2=\dfrac{16}{3} \\[4pt]
&\dfrac{9}{16}\left(x+\dfrac{2}{3}\right)^2-\dfrac{3}{16}y^2=1
\end{align*}

よって，点Pの軌跡は双曲線 $\dfrac{9}{16}\left(x+\dfrac{2}{3}\right)^2-\dfrac{3}{16}y^2=1$

離心率と二次曲線に関するまとめ

ヒロ

円錐の中心軸と母線のなす角を $\theta$ とし，切断する平面とのなす角を $\varphi$ とすると，円錐を平面で切断したときの断面は次のようになる。

円錐の切断面

　
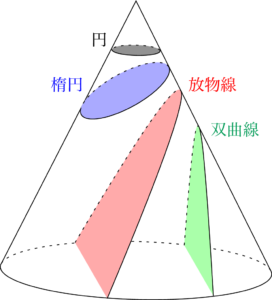
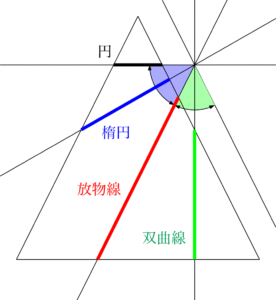
$0\leqq\varphi<\theta$ のとき
双曲線
$\varphi=\theta$ のとき
放物線
$\theta<\varphi<\dfrac{\pi}{2}$ のとき
楕円
$\varphi=\dfrac{\pi}{2}$ のとき
円

ヒロ

極方程式の離心率による分類も覚えておこう。

$r=\dfrac{l}{1-\varepsilon\cos\theta}$ が表す曲線

$0<\varepsilon<1$ のとき
楕円
$\varepsilon=1$ のとき
放物線
$1<\varepsilon$ のとき
双曲線

二次曲線の極方程式と離心率・半直弦

二次曲線の離心率に関する入試問題【2018年 札幌医科大】

離心率と二次曲線に関するまとめ

二次曲線の離心率に関する入試問題【2018年札幌医科大】