Contents
対数を指数関数のグラフから捉える

ヒロ
これまでに色々な指数を扱ってきた。ここで $2^x=6$ をみたす $x$ を考えることにする。

ヒロ
その前に,1つ余談を挟むことにする。
【間違えるのは読み方が原因】
$2^x=6$ をみたす $x$ を $x=3$ と思ってしまう人は,読み方が間違っていることが原因かもしれない。つまり,$2^x$ を「2の $x$ 乗」ではなく「2の $x$」と読んでいることが原因の1つだろう。$2^x=6$ を見て「2の $x$ が6」と読んでいるから,$x=3$ だと勘違いしてしまう。教える側が,元の $x$ に当てはめて確認するように指示したとしても,その人の頭の中では「2の3が6」となって何が間違っているのか分からない状態で,間違いを正すのは難しい。
「乗」まで読むように指示すると「2の3乗が6」となり,何を勘違いしていたかが分かるようになる。数式の意味を正しく理解すると,$2^x=6$ をみたす $x$ なんて分からないということになる。

ヒロ
それでは $2^x=6$ をみたす $x$ はどのような数かを考える。
【$2^x=6$ をみたす $x$ とは】
$y=2^x$ のグラフを描くと,$2^x=6$ をみたす $x$ は下図の黒丸の点の $x$ 座標 $a$ であることが分かる。
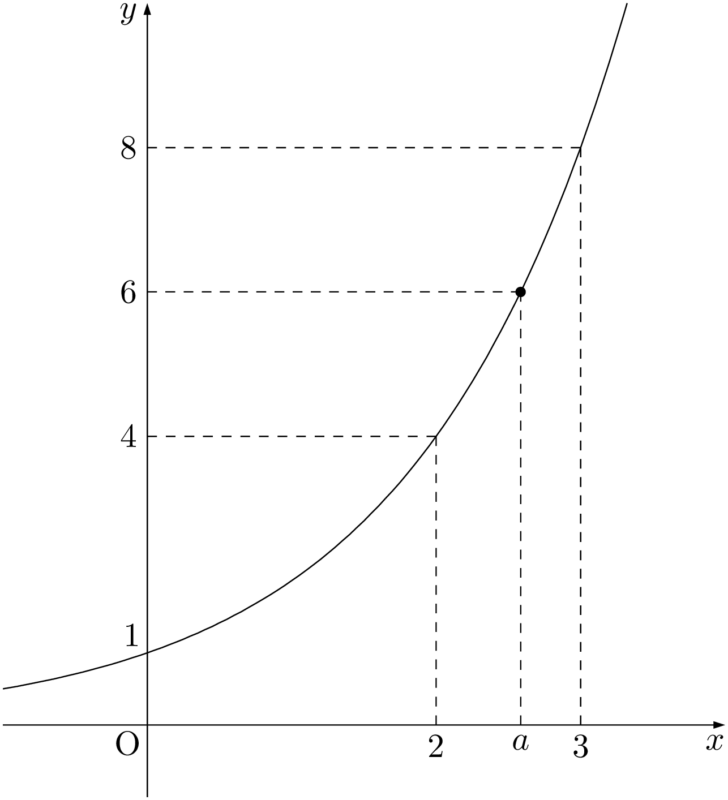
グラフより,$2^x=6$ をみたす $x=a$ は $2<a<3$ となることは分かるが,正確な値はよく分からない。そこで平方根のときと同じように,新しい記号を導入して「2を何乗かすると6になる数」を表すことにする。対数を意味する「logarithm」から $\log$ という記号を作り,「2を何乗かすると6になる数」を「$\log_26$」と表すことにした。ちなみに $\log_26$ は無理数であり,近似値は 2.5849 である。
$y=2^x$ のグラフを描くと,$2^x=6$ をみたす $x$ は下図の黒丸の点の $x$ 座標 $a$ であることが分かる。

グラフより,$2^x=6$ をみたす $x=a$ は $2<a<3$ となることは分かるが,正確な値はよく分からない。そこで平方根のときと同じように,新しい記号を導入して「2を何乗かすると6になる数」を表すことにする。対数を意味する「logarithm」から $\log$ という記号を作り,「2を何乗かすると6になる数」を「$\log_26$」と表すことにした。ちなみに $\log_26$ は無理数であり,近似値は 2.5849 である。
対数の意味を考える

ヒロ
対数の意味を考えることで,このあとで説明する対数法則も理解しやすくなるだろう。
【対数で表された数】
ある程度,累乗数を覚えておくことで,対数で表された数がどのような数であるかを瞬時に言えるようになることを知っておこう。
例えば,$\log_232$ がどのような数であるかを考える。これは「2を何乗すると32になるか?」と聞かれているのと同じである。$32=2^5$ であることが常識になっていれば,$\log_232=5$ であることがすぐに分かるだろう。
ある程度,累乗数を覚えておくことで,対数で表された数がどのような数であるかを瞬時に言えるようになることを知っておこう。
例えば,$\log_232$ がどのような数であるかを考える。これは「2を何乗すると32になるか?」と聞かれているのと同じである。$32=2^5$ であることが常識になっていれば,$\log_232=5$ であることがすぐに分かるだろう。

ヒロ
同じように考えて,次の問題を解いてみよう。
2020年 慶應義塾大$\log_327=\myhako$,$\log_5\dfrac{1}{25}=\myhako$,$\log_93=\myhako$ である。
【考え方と解答】
$\log_327$ は「3の何乗が27か?」と聞かれている。$27=3^3$ であるから,$\log_327=3$ である。
$\log_5\dfrac{1}{25}$ は「5の何乗が $\dfrac{1}{25}$ か?」と聞かれている。$\dfrac{1}{25}=5^{-2}$ であるから,$\log_5\dfrac{1}{25}=-2$ である。
$\log_93$ は「9の何乗が3か?」と聞かれている。$3=9^{\frac{1}{2}}$ であるから,$\log_93=\dfrac{1}{2}$ である。
$\log_327$ は「3の何乗が27か?」と聞かれている。$27=3^3$ であるから,$\log_327=3$ である。
$\log_5\dfrac{1}{25}$ は「5の何乗が $\dfrac{1}{25}$ か?」と聞かれている。$\dfrac{1}{25}=5^{-2}$ であるから,$\log_5\dfrac{1}{25}=-2$ である。
$\log_93$ は「9の何乗が3か?」と聞かれている。$3=9^{\frac{1}{2}}$ であるから,$\log_93=\dfrac{1}{2}$ である。


















