Contents
放物線 $y=ax^2+bx+c$ 上の2点を通る直線を簡単に求める方法

ヒロ
$y=ax^2+bx+c$ と $y=ax^2$ の違いは $bx+c$ の部分だから,この分だけずらせば良いね。

ヒロ
つまり,一般的な2次関数 $y=ax^2+bx+c$ 上の2点を通る直線の方程式は次のようになる。
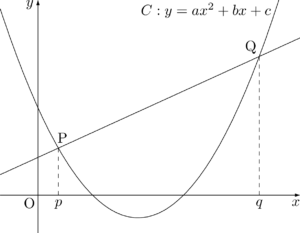
$y=ax^2+bx+c$ 上の2点を通る直線の方程式$f(x)=ax^2+bx+c$ とする。$y=f(x)$ 上の2点 $\mathrm{P}(p,~f(p))$, $\mathrm{Q}(q,~f(q))$ を通る直線の方程式は
\begin{align*}
&y={\color{blue}a(p+q)x-apq}+{\color{red}bx+c} \\[4pt]
&y=\{a(p+q)+b\}x-apq+c
\end{align*}
&y={\color{blue}a(p+q)x-apq}+{\color{red}bx+c} \\[4pt]
&y=\{a(p+q)+b\}x-apq+c
\end{align*}


ヒロ
この公式が正しいことを確認しておこう。
【正しいことの確認】
直線
$x=p$ を代入すると
直線
\begin{align*}
y=a(p+q)x-apq+bx+c \cdots\cdots(\ast)
\end{align*}
が2点P, Qを通ることを確認する。y=a(p+q)x-apq+bx+c \cdots\cdots(\ast)
\end{align*}
$x=p$ を代入すると
\begin{align*}
y&=a(p+q)p-apq+bp+c \\[4pt]
&=ap^2+bp+c
\end{align*}
また,$x=q$ を代入するとy&=a(p+q)p-apq+bp+c \\[4pt]
&=ap^2+bp+c
\end{align*}
\begin{align*}
y&=a(p+q)q-apq+bq+c \\[4pt]
&=aq^2+bq+c
\end{align*}
よって,$f(x)=ax^2+bx+c$ とすると,直線 $(\ast)$ は2点 $\mathrm{P}(p,~f(p))$, $\mathrm{Q}(q,~f(q))$ を通る。y&=a(p+q)q-apq+bq+c \\[4pt]
&=aq^2+bq+c
\end{align*}

ヒロ
これで,どんな放物線でも,その放物線上の2点を通る直線の方程式を簡単に求めることができるね。


















