苦手な人が多い問題の1つが,三角関数を含む不等式の表す領域の問題です。この記事で扱う問題は,2019年に大阪大学で出題されたものですが,阪大の入試問題だから無理だと思わずに取り組んで下さい。
例として阪大の入試問題を取り上げただけで,このレベルの問題であれば,どの大学でも出題される可能性があります。しっかり解けるようにしましょう。
2019年 大阪大$xy$ 平面において,連立不等式
(1) $D$ を図示せよ。
(2) 点 $(x,~y)$ が領域 $D$ を動くとき,$2x+y$ の最大値と最小値を求めよ。
\begin{align*}
&0\leqq x\leqq\pi,~0\leqq y\leqq\pi \\[4pt]&2\sin(x+y)-2\cos(x+y)\geqq\sqrt{2}
\end{align*}
の表す領域を $D$ とする。このとき以下の問いに答えよ。&0\leqq x\leqq\pi,~0\leqq y\leqq\pi \\[4pt]&2\sin(x+y)-2\cos(x+y)\geqq\sqrt{2}
\end{align*}
(1) $D$ を図示せよ。
(2) 点 $(x,~y)$ が領域 $D$ を動くとき,$2x+y$ の最大値と最小値を求めよ。

ヒロ
(1)の不等式の表す領域を図示するためには,三角関数の中身の角度に関する不等式を導く必要がある。
【(1)の解答】
\begin{align*}
&2\sin(x+y)-2\cos(x+y)\geqq\sqrt{2} \\[4pt]&2\sqrt{2}\sin\left(x+y-\dfrac{\pi}{4}\right)\geqq\sqrt{2} \\[4pt]&\sin\left(x+y-\dfrac{\pi}{4}\right)\geqq\dfrac{1}{2}
\end{align*}
$0\leqq x+y\leqq2\pi$ より&2\sin(x+y)-2\cos(x+y)\geqq\sqrt{2} \\[4pt]&2\sqrt{2}\sin\left(x+y-\dfrac{\pi}{4}\right)\geqq\sqrt{2} \\[4pt]&\sin\left(x+y-\dfrac{\pi}{4}\right)\geqq\dfrac{1}{2}
\end{align*}
\begin{align*}
&\dfrac{\pi}{6}\leqq x+y-\dfrac{\pi}{4}\leqq\dfrac{5}{6}\pi \\[4pt]&\dfrac{5}{12}\pi\leqq x+y\leqq\dfrac{13}{12}\pi
\end{align*}
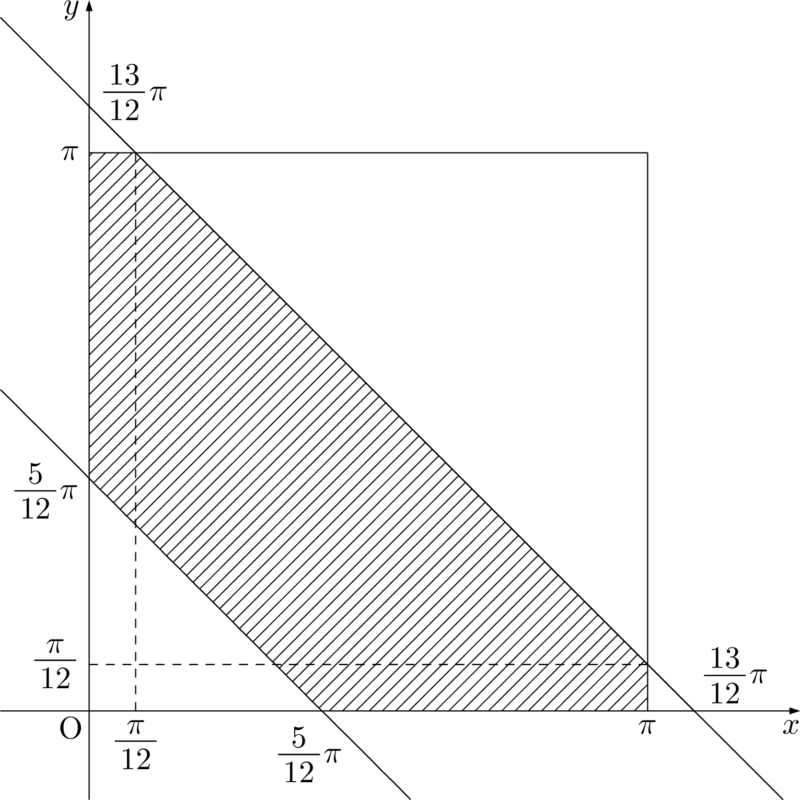
よって,求める領域 $D$ は図の斜線部分(境界を含む)となる。&\dfrac{\pi}{6}\leqq x+y-\dfrac{\pi}{4}\leqq\dfrac{5}{6}\pi \\[4pt]&\dfrac{5}{12}\pi\leqq x+y\leqq\dfrac{13}{12}\pi
\end{align*}


ヒロ
(2)は $x,~y$ の2つの変数を含む式の最大最小問題だから,$2x+y=k$ とおいて,1つの変数 $k$ の動きをみるようにしよう。

ヒロ
また,$2x+y=k$ とおくことで,これは $xy$ 平面上で直線を表す。(1)で図示した領域を活用することができる。
【(2)の解答】
$2x+y=k$ とおくと,$y=-2x+k$ となり,これは傾き $-2$,$y$ 切片 $k$ の直線を表す。よって,$k$ が最大になるのは,この直線が点 $\left(\pi,~\dfrac{\pi}{12}\right)$ を通るときであり,$k$ が最小になるのは,この直線が点 $\left(0,~\dfrac{5}{12}\pi\right)$ を通るときである。
したがって,求める最大値は $\dfrac{25}{12}\pi$ であり,最小値は $\dfrac{5}{12}\pi$ である。
$2x+y=k$ とおくと,$y=-2x+k$ となり,これは傾き $-2$,$y$ 切片 $k$ の直線を表す。よって,$k$ が最大になるのは,この直線が点 $\left(\pi,~\dfrac{\pi}{12}\right)$ を通るときであり,$k$ が最小になるのは,この直線が点 $\left(0,~\dfrac{5}{12}\pi\right)$ を通るときである。
したがって,求める最大値は $\dfrac{25}{12}\pi$ であり,最小値は $\dfrac{5}{12}\pi$ である。

ヒロ
それほど難しい問題ではないため,しっかり解けるようにしておこう。


















