ここでは条件付き確率について解説します。
確率を考えるときには,特定の条件の下での確率を求めたい場合があります。
条件付き確率事象 $A$ が起こったときに事象 $B$ が起こる確率を「事象 $A$ が起こったときの事象 $B$ が起こる条件付き確率」といい,$P_A(B)$ で表し,
\begin{align*}
P_A(B)=\dfrac{P(A\cap B)}{P(A)}
\end{align*}
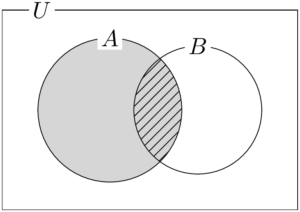
これは事象 $A$ を全体と見て,その中で事象 $B$ が起こる確率を考えている。ベン図で考えると分かりやすいかもしれない。灰色部分のうち斜線部分がどれくらいの割合かを考えれば良い。P_A(B)=\dfrac{P(A\cap B)}{P(A)}
\end{align*}

実際に定期テストで出題された問題を扱って説明していきます。
条件付き確率を求める問題
問題二つの袋甲・乙がある。甲には赤玉3個と白玉3個が入っており,乙には赤玉5個と白玉4個が入っている。さいころを投げて,1, 2の目が出たら甲,それ以外の目が出たら乙から玉を1個取り出す。このとき,次の問いに答えよ。
(1) 白玉を取り出す確率を求めよ。
(2) 白玉を取り出したとき,それが乙の袋から取り出された玉である確率を求めよ。
(1) 白玉を取り出す確率を求めよ。
(2) 白玉を取り出したとき,それが乙の袋から取り出された玉である確率を求めよ。
【(1)の考え方と解答】
白玉を取り出すのは次の2つの場合がある。
(i) 甲から白玉を取り出す
(ii) 乙から白玉を取り出す
(i)が起こるのは,1, 2の目が出て甲から白玉を取り出すときだから,その確率は
白玉を取り出すのは次の2つの場合がある。
(i) 甲から白玉を取り出す
(ii) 乙から白玉を取り出す
(i)が起こるのは,1, 2の目が出て甲から白玉を取り出すときだから,その確率は
\begin{align*}
\dfrac{2}{6}\times\dfrac{3}{6}=\dfrac{1}{6}
\end{align*}
(ii)が起こるのは,1, 2以外の目が出て乙から白玉を取り出すときだから,その確率は\dfrac{2}{6}\times\dfrac{3}{6}=\dfrac{1}{6}
\end{align*}
\begin{align*}
\dfrac{4}{6}\times\dfrac{4}{9}=\dfrac{8}{27}
\end{align*}
(i), (ii)より,求める確率は\dfrac{4}{6}\times\dfrac{4}{9}=\dfrac{8}{27}
\end{align*}
\begin{align*}
\dfrac{1}{6}+\dfrac{8}{27}=\dfrac{25}{54}
\end{align*}
\dfrac{1}{6}+\dfrac{8}{27}=\dfrac{25}{54}
\end{align*}
(2) 白玉を取り出したとき,それが乙の袋から取り出された玉である確率を求めよ。
【(2)の考え方と解答】
白球を取り出すという事象を $A$,乙の袋から取り出すという事象を $B$ とすると,求める確率は,$A$ を全事象とした場合の事象 $A\cap B$ の起こる確率であるから
白球を取り出すという事象を $A$,乙の袋から取り出すという事象を $B$ とすると,求める確率は,$A$ を全事象とした場合の事象 $A\cap B$ の起こる確率であるから
\begin{align*}
P_A(B)=\dfrac{P(A\cap B)}{P(A)}
\end{align*}
で表される。ここで(1)よりP_A(B)=\dfrac{P(A\cap B)}{P(A)}
\end{align*}
\begin{align*}
P(A)=\dfrac{25}{54},~P(A\cap B)=\dfrac{8}{27}
\end{align*}
であるからP(A)=\dfrac{25}{54},~P(A\cap B)=\dfrac{8}{27}
\end{align*}
\begin{align*}
P_A(B)&=\dfrac{\dfrac{8}{27}}{\dfrac{25}{54}} \\[4pt]
&=\dfrac{16}{25}
\end{align*}
P_A(B)&=\dfrac{\dfrac{8}{27}}{\dfrac{25}{54}} \\[4pt]
&=\dfrac{16}{25}
\end{align*}
条件付き確率を求める問題2
問題白玉5個,赤玉2個が入った袋から,もとに戻さないで1個ずつ続けて2回玉を取り出す。2回目の玉が赤玉であるとき,1回目の玉も赤玉である確率を求めよ。
【考え方と解答】
1回目の玉が赤玉である事象を $A$,2回目の玉が赤玉である事象を $B$ とすると,求める確率は,
① 1回目の玉が赤玉で,2回目の玉も赤玉
② 1回目の玉が白玉で,2回目の玉も赤玉
①が起こる確率は $P(A\cap B)$ で
1回目の玉が赤玉である事象を $A$,2回目の玉が赤玉である事象を $B$ とすると,求める確率は,
\begin{align*}
P_B(A)=\dfrac{P(B\cap A)}{P(B)}
\end{align*}
で求められる。2回目の玉が赤玉であるのは次の2つの場合がある。P_B(A)=\dfrac{P(B\cap A)}{P(B)}
\end{align*}
① 1回目の玉が赤玉で,2回目の玉も赤玉
② 1回目の玉が白玉で,2回目の玉も赤玉
①が起こる確率は $P(A\cap B)$ で
\begin{align*}
P(A\cap B)=\dfrac{2}{7}\times\dfrac{1}{6}=\dfrac{1}{21}
\end{align*}
②が起こる確率はP(A\cap B)=\dfrac{2}{7}\times\dfrac{1}{6}=\dfrac{1}{21}
\end{align*}
\begin{align*}
\dfrac{5}{7}\times\dfrac{2}{6}=\dfrac{5}{21}
\end{align*}
したがって,2回目の玉が赤玉である確率 $P(B)$ は\dfrac{5}{7}\times\dfrac{2}{6}=\dfrac{5}{21}
\end{align*}
\begin{align*}
P(B)&=\dfrac{1}{21}+\dfrac{5}{21}=\dfrac{6}{21}
\end{align*}
よって,求める確率はP(B)&=\dfrac{1}{21}+\dfrac{5}{21}=\dfrac{6}{21}
\end{align*}
\begin{align*}
\dfrac{\dfrac{1}{21}}{\dfrac{6}{21}}=\dfrac{1}{6}
\end{align*}
\dfrac{\dfrac{1}{21}}{\dfrac{6}{21}}=\dfrac{1}{6}
\end{align*}
条件付き確率を求める問題3
問題1から20までの番号が書かれた札が入っている箱がある。この箱から1枚ずつ順に,取り出した札を戻さないで2枚を取り出したところ,2枚の中に3の倍数の札があった。このとき,2枚目の札が3の倍数の札である確率を求めよ。
【考え方と解答】
2枚の中に3の倍数の札がある事象を $A$,2枚目の札が3の倍数である事象を $B$ とすると,求める確率は
① 2枚の札がともに3の倍数である
② 1枚目の札が3の倍数でなく,2枚目の札が3の倍数である
①が起こる確率は
2枚の中に3の倍数の札がある事象を $A$,2枚目の札が3の倍数である事象を $B$ とすると,求める確率は
\begin{align*}
P_A(B)=\dfrac{P(A\cap B)}{P(A)}
\end{align*}
で求められる。まず $A$ が起こる確率 $P(A)$ を求める。2枚の札のうち少なくとも1枚の札が3の倍数である確率である。「少なくとも」とくれば余事象を考えてみることも重要で,余事象が起こる確率は「2枚の札がともに3の倍数でない確率」である。20以下の自然数で3の倍数は6個あるから,3の倍数でない数は14個ある。したがって,$P(A)$ はP_A(B)=\dfrac{P(A\cap B)}{P(A)}
\end{align*}
\begin{align*}
P(A)&=1-\dfrac{14\Cdot13}{20\Cdot19} \\[4pt]
&=1-\dfrac{91}{190}=\dfrac{99}{190}
\end{align*}
次に $P(A\cap B)$ を求める。$A\cap B$ は次の2つの事象を表す。P(A)&=1-\dfrac{14\Cdot13}{20\Cdot19} \\[4pt]
&=1-\dfrac{91}{190}=\dfrac{99}{190}
\end{align*}
① 2枚の札がともに3の倍数である
② 1枚目の札が3の倍数でなく,2枚目の札が3の倍数である
①が起こる確率は
\begin{align*}
\dfrac{6}{20}\times\dfrac{5}{19}=\dfrac{15}{190}
\end{align*}
②が起こる確率は\dfrac{6}{20}\times\dfrac{5}{19}=\dfrac{15}{190}
\end{align*}
\begin{align*}
\dfrac{14}{20}\times\dfrac{6}{19}=\dfrac{42}{190}
\end{align*}
よって\dfrac{14}{20}\times\dfrac{6}{19}=\dfrac{42}{190}
\end{align*}
\begin{align*}
P(A\cap B)&=\dfrac{15}{190}+\dfrac{42}{190} \\[4pt]
&=\dfrac{57}{190}=\dfrac{3}{10}
\end{align*}
よって,求める確率はP(A\cap B)&=\dfrac{15}{190}+\dfrac{42}{190} \\[4pt]
&=\dfrac{57}{190}=\dfrac{3}{10}
\end{align*}
\begin{align*}
\dfrac{\dfrac{3}{10}}{\dfrac{99}{190}}=\dfrac{19}{33}
\end{align*}
\dfrac{\dfrac{3}{10}}{\dfrac{99}{190}}=\dfrac{19}{33}
\end{align*}



















