Contents
放物線上の2点を通る直線の式を求める練習問題

ヒロ
最後に1問練習しておこう。
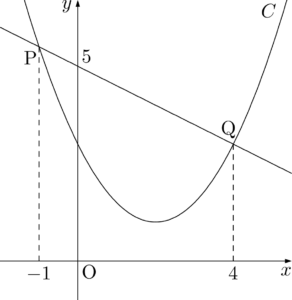
練習問題放物線 $C:y=\dfrac{1}{2}x^2-2x+3$ 上の2点P, Qの $x$ 座標をそれぞれ $-1,~4$ とするとき,直線PQの方程式を求めよ。
【解答】
求める直線PQの方程式は
求める直線PQの方程式は
\begin{align*}
&y=\dfrac{1}{2}(-1+4)x-\dfrac{1}{2}\Cdota(-1)\Cdota4-2x+3 \\[4pt]
&y=\dfrac{3}{2}x+2-2x+3 \\[4pt]
&y=-\dfrac{1}{2}x+5
\end{align*}
&y=\dfrac{1}{2}(-1+4)x-\dfrac{1}{2}\Cdota(-1)\Cdota4-2x+3 \\[4pt]
&y=\dfrac{3}{2}x+2-2x+3 \\[4pt]
&y=-\dfrac{1}{2}x+5
\end{align*}


ヒロ
簡単なので,すぐに使いこなせるようになるだろう。
放物線上の2点を通る直線の式を簡単に求める方法のまとめ

ヒロ
$y=ax^2$ 上の2点を通る直線を簡単に求める方法は有名である。

ヒロ
一般的な放物線上の2点を通る直線も簡単に求めることができることを知っておこう。
【放物線上の2点を通る直線を簡単に求める方法】
$f(x)=ax^2+bx+c$ とする。$y=f(x)$ 上の2点 $\mathrm{P}(p,~f(p))$, $\mathrm{Q}(q,~f(q))$ を通る直線の方程式は
$f(x)=ax^2+bx+c$ とする。$y=f(x)$ 上の2点 $\mathrm{P}(p,~f(p))$, $\mathrm{Q}(q,~f(q))$ を通る直線の方程式は
\begin{align*}
&y={\color{blue}a(p+q)x-apq}+{\color{red}bx+c} \\[4pt]
&y=\{a(p+q)+b\}x-apq+c
\end{align*}
&y={\color{blue}a(p+q)x-apq}+{\color{red}bx+c} \\[4pt]
&y=\{a(p+q)+b\}x-apq+c
\end{align*}



















