Contents
楕円の媒介変数表示

ヒロ
楕円上の点を媒介変数 $\theta$ を用いて表そう。
原点を中心とする半径 $a$ の円 $C$ を考える。円周上の点Qに対して,OQと $x$ 軸の正の方向のなす角を $\theta$ とし,点Qを通り $x$ 軸に垂直な直線と楕円の交点をP,$x$ 軸との交点をHとする。
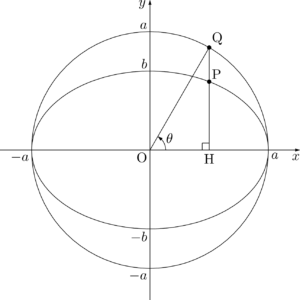
このとき,点Pの $x$ 座標は点Qの $x$ 座標と等しいから $a\cos\theta$ である。
ここで,楕円の方程式 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ を $y~(\geqq0)$ について解くと

このとき,点Pの $x$ 座標は点Qの $x$ 座標と等しいから $a\cos\theta$ である。
ここで,楕円の方程式 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ を $y~(\geqq0)$ について解くと
\begin{align*}
y=\dfrac{b}{a}\sqrt{a^2-x^2}
\end{align*}
となり,これは円 $C$ を $y$ 軸方向へ $\dfrac{b}{a}$ 倍にしたことを表しているから,点Pの $y$ 座標はy=\dfrac{b}{a}\sqrt{a^2-x^2}
\end{align*}
\begin{align*}
a\sin\theta\times\dfrac{b}{a}
\end{align*}
となる。よって,楕円の媒介変数表示は次のようになる。a\sin\theta\times\dfrac{b}{a}
\end{align*}
\begin{align*}
x=a\cos\theta,~~y=b\sin\theta
\end{align*}
x=a\cos\theta,~~y=b\sin\theta
\end{align*}

ヒロ
楕円の極座標表示においてよくある間違いは,$\theta=\kaku{POH}$ と解釈してしまうこと。実際の $\theta$ は $\kaku{QOH}$ を表している。

ヒロ
$\theta$ を求める問題などで,$\theta=\dfrac{\pi}{3}$ のような有名角が出てきた場合,三平方の定理などで検算して「何これ・・・合わないんだけど」となってしまう人もいる。求めた角度と自分が考えている角度が違っていることが原因なので,正しく知ることで無駄に悩む時間を減らそう。


















