Contents
楕円の焦点の覚え方

ヒロ
楕円の方程式 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ が与えられたときに焦点の座標がパッと出てこないことがある。また「楕円の焦点の座標を覚えられない」とか「すぐ忘れる」って言う人は楕円の定義からサクッと求められるようにしておこう。
楕円上に点Pをとったとき,2つの焦点F, F$’$ までの距離の和が一定だから,その距離の和を計算しやすい点を考えよう。ここで,焦点Fの $x$ 座標 $c$ は正とする。
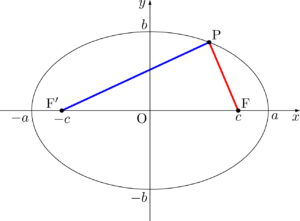
点Pを $(a,~0)$ にとったとき,
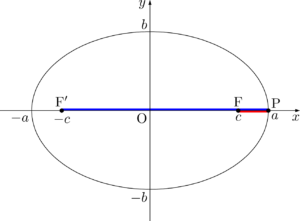
次に点Pを $(0,~b)$ にとったときを考える。
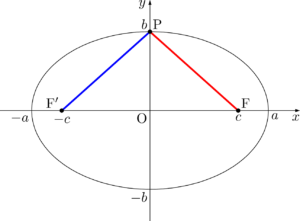
$\mathrm{PF}=\mathrm{PF’}$ より $\mathrm{PF}=a$ となる。ここで,直角三角形OFPに着目する。
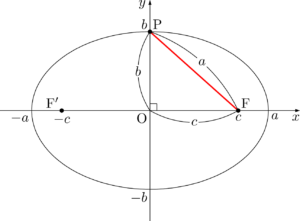
三平方の定理より,$b^2+c^2=a^2$ が成り立つから,これを解いて,

点Pを $(a,~0)$ にとったとき,
\begin{align*}
\mathrm{PF}+\mathrm{PF’}=2a
\end{align*}
であることがすぐに分かる。\mathrm{PF}+\mathrm{PF’}=2a
\end{align*}

次に点Pを $(0,~b)$ にとったときを考える。

$\mathrm{PF}=\mathrm{PF’}$ より $\mathrm{PF}=a$ となる。ここで,直角三角形OFPに着目する。

三平方の定理より,$b^2+c^2=a^2$ が成り立つから,これを解いて,
\begin{align*}
c=\sqrt{a^2-b^2}
\end{align*}
となる。c=\sqrt{a^2-b^2}
\end{align*}

ヒロ
これで焦点Fの座標が $(\sqrt{a^2-b^2},~0)$ であると分かるが,「たったこれだけ」と思うか「こんなに計算するのか」と思うのかは人それぞれ。

ヒロ
忘れないことも重要であるが,忘れたときの対処法を用意しておくことも重要。


















