Contents
楕円に関する入試問題【2018年 大阪教育大】
2018年 大阪教育大$\alpha$ を複素数,$r$ を正の数とする。ただし,$\abs{\alpha}\neq r$ とする。複素数平面上で
(1) 等式を満たす点 $z$ が存在するための条件を $\alpha,~r$ を用いて表せ。そのとき,どのような図形を表すか。
(2) (1)の条件を満たすとき,等式を満たす点 $z$ の絶対値の最大値と最小値を求めよ。
(3) 等式を満たす点 $z$ の全体が表す図形で囲まれた部分の面積 $S$ を求めよ。
\begin{align*}
\abs{z-\alpha}+\abs{z+\alpha}=2r
\end{align*}
を満たす点 $z$ を考える。\abs{z-\alpha}+\abs{z+\alpha}=2r
\end{align*}
(1) 等式を満たす点 $z$ が存在するための条件を $\alpha,~r$ を用いて表せ。そのとき,どのような図形を表すか。
(2) (1)の条件を満たすとき,等式を満たす点 $z$ の絶対値の最大値と最小値を求めよ。
(3) 等式を満たす点 $z$ の全体が表す図形で囲まれた部分の面積 $S$ を求めよ。

ヒロ
与えられた等式を見て,すぐに楕円を描くということに気付けるようにしよう。
【(1)の解答】
複素数平面上の3点P, A, Bを $\mathrm{P}(z)$, $\mathrm{A}(\alpha)$, $\mathrm{B}(-\alpha)$ とすると,
複素数平面上の3点P, A, Bを $\mathrm{P}(z)$, $\mathrm{A}(\alpha)$, $\mathrm{B}(-\alpha)$ とすると,
\begin{align*}
\abs{z-\alpha}+\abs{z+\alpha}=\mathrm{PA}+\mathrm{PB}
\end{align*}
となり,点Pの位置を変えることで $\mathrm{PA}+\mathrm{PB}$ をいくらでも大きくすることができる。また三角不等式より\abs{z-\alpha}+\abs{z+\alpha}=\mathrm{PA}+\mathrm{PB}
\end{align*}
\begin{align*}
\mathrm{PA}+\mathrm{PB}\geqq\mathrm{AB}=2\abs{\alpha}
\end{align*}
が成り立つから,\mathrm{PA}+\mathrm{PB}\geqq\mathrm{AB}=2\abs{\alpha}
\end{align*}
\begin{align*}
\abs{z-\alpha}+\abs{z+\alpha}=2r
\end{align*}
を満たす点 $z$ が存在するための条件は\abs{z-\alpha}+\abs{z+\alpha}=2r
\end{align*}
\begin{align*}
&2r\geqq2\abs{\alpha} \\[4pt]
&r\geqq\abs{\alpha}
\end{align*}
を満たすことである。ここで $\abs{\alpha}\neq r$ であるから,求める条件は&2r\geqq2\abs{\alpha} \\[4pt]
&r\geqq\abs{\alpha}
\end{align*}
\begin{align*}
r>\abs{\alpha}
\end{align*}
である。このとき,点 $z$ は2点 $\alpha,~-\alpha$ を焦点とする長軸の長さが $2r$ の楕円を描く。r>\abs{\alpha}
\end{align*}

ヒロ
楕円の長軸と短軸の交点が原点であることと,$\abs{z}$ は原点から点 $z$ までの距離であることが分かっていれば簡単だね。
【(2)の解答】
点 $z$ が描く楕円の長半径は $r$ であり,短半径は $\sqrt{r^2-\abs{\alpha}^2}$ である。よって,$\abs{z}$ の最大値は $r$,最小値は $\sqrt{r^2-\abs{\alpha}^2}$ である。
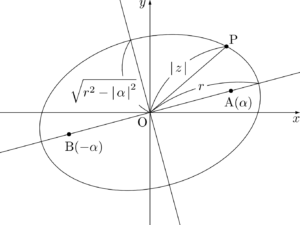
点 $z$ が描く楕円の長半径は $r$ であり,短半径は $\sqrt{r^2-\abs{\alpha}^2}$ である。よって,$\abs{z}$ の最大値は $r$,最小値は $\sqrt{r^2-\abs{\alpha}^2}$ である。


ヒロ
(3)は楕円の面積公式でサクッと求めよう。
【(3)の解答】
\begin{align*}
S&=\pi r\sqrt{r^2-\abs{\alpha}^2}
\end{align*}
S&=\pi r\sqrt{r^2-\abs{\alpha}^2}
\end{align*}
楕円の性質についてのまとめ

ヒロ
楕円の性質についてまとめると次のようになる。
$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$
- グラフ
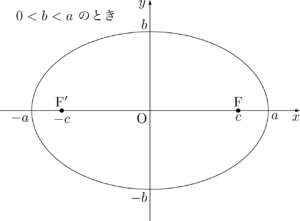
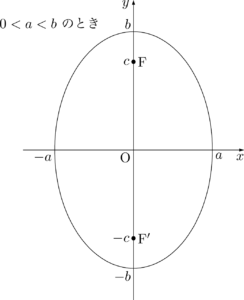
- 焦点の座標
$0<b<a$ のとき\begin{align*}$0<a<b$ のとき
\mathrm{F}(\sqrt{a^2-b^2},~0),~\mathrm{F}'(-\sqrt{a^2-b^2},~0)
\end{align*}\begin{align*}
\mathrm{F}(0,~\sqrt{b^2-a^2}),~\mathrm{F}'(0,~-\sqrt{b^2-a^2})
\end{align*} - 極方程式\begin{align*}ここで $\varepsilon$ と $l$ はそれぞれ離心率,半直弦と呼ばれる定数であり,
r=\dfrac{l}{1+\varepsilon \cos\theta}
\end{align*}\begin{align*}で定められる。
&0<b<a~のとき,\varepsilon=\dfrac{\sqrt{a^2-b^2}}{a},~l=\dfrac{b^2}{a} \\[4pt]
&0<a<b~のとき,\varepsilon=\dfrac{\sqrt{b^2-a^2}}{a},~l=\dfrac{a^2}{b}
\end{align*} - 媒介変数表示\begin{align*}
x=a\cos\theta,~~y=b\sin\theta
\end{align*} - 接線の方程式\begin{align*}
\dfrac{x_1x}{a^2}+\dfrac{y_1y}{b^2}=1
\end{align*} - 面積 $S$\begin{align*}
S=\pi ab
\end{align*}


















