2003年センター試験 数学ⅡB 第1問 複素数平面の解説をします。
まだ問題を解いていない人は解いてから解説を読んでください。
&z_0=(\sqrt3+i)(\polar\theta) \\[4pt]
&z_1=\dfrac{4\{(1-\sin\theta)+i\cos\theta\}}{(1-\sin\theta)-i\cos\theta} \\[4pt]
&z_2=-\dfrac{2}{z_1}
\end{align*}
(1) $\abs{z_0}=\myBox{ア}$, $\arg z_0=\myBox{イウ}\Deg+\theta$ である。
(2) $z_1$ の分母と分子に $(1-\sin\theta)+i\cos\theta$ をかけて計算すると
z_1=\myBox{エ}(-\sin\theta+i\cos\theta)
\end{align*}
(3) $\abs{\dfrac{z_1}{z_0}}=\myBox{ク}$, $\arg\dfrac{z_1}{z_0}=\myBox{ケコ}\Deg$ であるから,$\mathrm{P}_0\mathrm{P}_1=\myBox{サ}\sqrt{\myBox{シ}}$ である。
(4) 原点O, $\mathrm{P}_0$, $\mathrm{P}_1$, $\mathrm{P}_2$ の4点が同一円周上にある場合を考える。 このとき $\kaku{OP_2P_1}$ を考えると
\arg\dfrac{z_1-z_2}{-z_2}=-\myBox{スセ}\Deg
\end{align*}
\myBox{ソ}\cos2\theta-\myBox{タ}=0
\end{align*}
\sin\theta=\dfrac{\sqrt{\myBox{チ}}}{\myBox{ツ}}
\end{align*}
(1)の解答

(1)は複素数の絶対値と偏角を求める問題。
$\abs{\sqrt{3}+i}=\sqrt{(\sqrt{3})^2+1^2}=2$, $\abs{\polar{\theta}}=1$ より
\abs{z_0}&=\abs{(\sqrt3+i)(\polar\theta)} \\[4pt]
&=\abs{(\sqrt3+i)}\abs{(\polar\theta)} \\[4pt]
&=2\Cdota1=2
\end{align*}
\sqrt{3}+i&=2\left(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}i\right) \\[4pt]
&=2(\polar{30\Deg})
\end{align*}
\arg z_0&=\arg(\sqrt3+i)(\polar\theta) \\[4pt]
&=\arg(\sqrt{3}+i)+\arg(\polar\theta) \\[4pt]
&=30\Deg+\theta
\end{align*}
(2)の解答
(2) $z_1$ の分母と分子に $(1-\sin\theta)+i\cos\theta$ をかけて計算すると
\begin{align*}となる。よって,$\abs{z_1}=\myBox{オ}$, $\arg z_1=\myBox{カキ}\Deg+\theta$ である。
z_1=\myBox{エ}(-\sin\theta+i\cos\theta)
\end{align*}

次は $z_1$ の絶対値と偏角を求める準備として $z_1$ を変形する問題。
$z_1$ の分母分子に $(1-\sin\theta)+i\cos\theta$ をかけると
z_1&=\dfrac{4\{(1-\sin\theta)+i\cos\theta\}^2}{(1-\sin\theta)^2+\cos^2\theta} \\[4pt]
&=\dfrac{4\{(1-\sin\theta)^2-\cos^2\theta+2i(1-\sin\theta)\cos\theta\}}{2(1-\sin\theta)} \\[4pt]
&=\dfrac{2\{(1-\sin\theta)^2-(1-\sin\theta)(1+\sin\theta)+2i(1-\sin\theta)\cos\theta\}}{1-\sin\theta} \\[4pt]
&=2\{(1-\sin\theta)-(1+\sin\theta)+2i\cos\theta\} \\[4pt]
&=4(-\sin\theta+i\cos\theta)
\end{align*}

スッキリした形になったから,絶対値と偏角を求めよう。
\abs{z_1}&=4\abs{-\sin\theta+i\cos\theta} \\[4pt]
&=4\sqrt{\sin^2\theta+\cos^2\theta}=4
\end{align*}
-\sin\theta+i\cos\theta&=\polar{(90\Deg+\theta)}
\end{align*}
\arg z_1&=\arg\{4(\polar{(90\Deg+\theta)})\} \\[4pt]
&=\arg\{\polar{(90\Deg+\theta)}\} \\[4pt]
&=90\Deg+\theta
\end{align*}
(3)の解答
(3) $\abs{\dfrac{z_1}{z_0}}=\myBox{ク}$, $\arg\dfrac{z_1}{z_0}=\myBox{ケコ}\Deg$ であるから,$\mathrm{P}_0\mathrm{P}_1=\myBox{サ}\sqrt{\myBox{シ}}$ である。

(1),(2)の結果を利用して,絶対値と偏角を求めよう。
(1),(2)の結果より
\abs{\dfrac{z_1}{z_0}}=\dfrac{4}{2}=2
\end{align*}
\arg\dfrac{z_1}{z_0}&=\arg z_1-\arg z_0 \\[4pt]&=(90\Deg+\theta)-(30\Deg+\theta) \\[4pt]&=60\Deg
\end{align*}

いま計算して求めた値の意味を考えて線分の長さを求めよう。
$\abs{\dfrac{z_1}{z_0}}=2$ より
&\dfrac{\mathrm{OP}_1}{\mathrm{OP}_2}=2 \\[4pt]&\mathrm{OP}_1=2\mathrm{OP}_2
\end{align*}
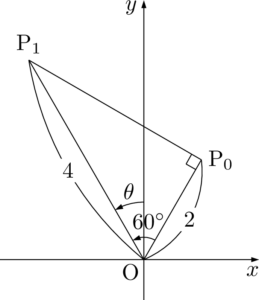
$\mathrm{OP}_0=2$ より,
\mathrm{P}_0\mathrm{P}_1=\sqrt{3}\mathrm{OP}_0=2\sqrt{3}
\end{align*}
(4)の解答
(4) 原点O, $\mathrm{P}_0$, $\mathrm{P}_1$, $\mathrm{P}_2$ の4点が同一円周上にある場合を考える。このとき $\kaku{OP_2P_1}$ を考えると
\begin{align*}であるから,
\arg\dfrac{z_1-z_2}{-z_2}=-\myBox{スセ}\Deg
\end{align*}\begin{align*}が成り立つ。よって
\myBox{ソ}\cos2\theta-\myBox{タ}=0
\end{align*}\begin{align*}となる。
\sin\theta=\dfrac{\sqrt{\myBox{チ}}}{\myBox{ツ}}
\end{align*}

4点が同一円周上にあることを数式で表現できるか問われているね。

着目する角も与えられているから簡単だろう。
$\sankaku{OP_0P_1}$ は $\kaku{OP_0P_1}=90\Deg$ の直角三角形だから,$\sankaku{OP_0P_1}$ の外接円は $\mathrm{OP}_1$ を直径とする円である。
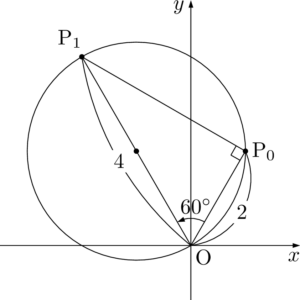
したがって, 原点O, $\mathrm{P}_0$, $\mathrm{P}_1$, $\mathrm{P}_2$ の4点が同一円周上にあるとき,$\mathrm{P}_2$ も $\sankaku{OP_0P_1}$ の外接円周上にある。ここで
z_2&=\dfrac{-2}{z_1} \\[4pt]&=\dfrac{2(\polar{180\Deg})}{4(\polar{(90\Deg+\theta)})} \\[4pt]&=\dfrac{1}{2}\{\polar{(90\Deg-\theta)}\}
\end{align*}
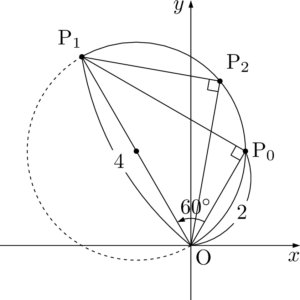
$\kaku{OP_2P_1}=90\Deg$ であり,$\Vec{P_2O}$ から $\Vec{P_2P_1}$ への回転は時計まわりだから
&\arg\dfrac{z_1-z_2}{0-z_2}=-90\Deg \\[4pt]&\arg\dfrac{z_1-z_2}{-z_2}=-90\Deg
\end{align*}

偏角が $-90\Deg$ であることから何が言えるのか考えよう。
偏角が $-90\Deg$ であるとき,実部は0であるから,$\dfrac{z_1-z_2}{-z_2}$ の実部を求めることから始めよう。
\dfrac{z_1-z_2}{-z_2}&=\dfrac{z_1+\dfrac{2}{z_1}}{\dfrac{2}{z_1}} \\[4pt]&=\dfrac{{z_1}^2+2}{2} \\[4pt]&=\dfrac{16(-\sin\theta+i\cos\theta)^2+2}{2} \\[4pt]&=8(\sin^2\theta-\cos^2\theta-2i\sin\theta\cos\theta)+1 \\[4pt]&=-8\cos2\theta+1-8i\sin2\theta
\end{align*}
&-8\cos2\theta+1=0 \\[4pt]&8\cos2\theta-1=0
\end{align*}

最後は $\cos2\theta$ の値から $\sin\theta$ の値を求める問題。

ここまで解けている人なら2倍角の公式も大丈夫だから,ボーナス問題だね。
$\cos2\theta=1-2\sin^2\theta$ であるから
&8(1-2\sin^2\theta)-1=0 \\[4pt]&\sin^2\theta=\dfrac{7}{16} \\[4pt]&\sin\theta=\pm\dfrac{\sqrt{7}}{4}
\end{align*}
\sin\theta=\dfrac{\sqrt{7}}{4}
\end{align*}
2003年 センター数学ⅡB 複素数平面を解いた感想

ド・モアブルの定理だけでなく,素早く計算する力が要求される。

後半は複素数と図の関連の理解が問われる問題になっているため,単に計算できるというだけでは苦労するだろう。

様々な知識がないと解けないように作られているため,複素数平面の復習をするのに良い練習になるだろう。





















