大学入試の数学の問題には,2つの数の大小を比較する問題が良く出ます。
ここでは累乗で表された2つの数の大小を比較する問題の解説をします。
簡単に理解できる考え方の問題もあれば,少し難しい考え方もありますが,1つずつ習得していくつもりで学習しましょう。
2008年 名古屋市立大・医

ヒロ
それでは次の問題を解いてみよう。
2008年 名古屋市立大・医次の問いに答えよ。ただし,必要に応じて次の値を使用してよい。
(2) $999^{1000}$ と $1000^{999}$ の大小を比較せよ。
\begin{align*}
&\log_{10}2=0.3010,~\log_{10}3=0.4771,~\log_{10}5=0.6990,~ \\[4pt]
&\log_{10}7=0.8451,~\log_{10}11=1.0414
\end{align*}
(1) $99^{100}$ と $100^{99}$ の大小を比較せよ。&\log_{10}2=0.3010,~\log_{10}3=0.4771,~\log_{10}5=0.6990,~ \\[4pt]
&\log_{10}7=0.8451,~\log_{10}11=1.0414
\end{align*}
(2) $999^{1000}$ と $1000^{999}$ の大小を比較せよ。
(1)の考え方と解答

ヒロ
問題文で与えられているいくつかの常用対数の値を利用しよう。

対数法則を使って計算するだけですね。
対数法則
\begin{align*}
&\log_aPQ=\log_aP+\log_aQ \\[4pt]
&\log_a\dfrac{P}{Q}=\log_aP-\log_aQ \\[4pt]
&\log_aP^k=k\log_aP
\end{align*}
&\log_aPQ=\log_aP+\log_aQ \\[4pt]
&\log_a\dfrac{P}{Q}=\log_aP-\log_aQ \\[4pt]
&\log_aP^k=k\log_aP
\end{align*}

ヒロ
解答を書いていこう。
【(1)の解答】
\begin{align*}
\log_{10}100^{99}&=99\times2=198 \\[4pt]
\log_{10}99^{100}&=100(2\log_{10}3+\log_{10}11) \\[4pt]
&=100(2\times0.4771+1.0414) \\[4pt]
&=199.56
\end{align*}
であるから,\log_{10}100^{99}&=99\times2=198 \\[4pt]
\log_{10}99^{100}&=100(2\log_{10}3+\log_{10}11) \\[4pt]
&=100(2\times0.4771+1.0414) \\[4pt]
&=199.56
\end{align*}
\begin{align*}
&\log_{10}99^{100}>\log_{10}100^{99} \\[4pt]
&99^{100}>100^{99}
\end{align*}
&\log_{10}99^{100}>\log_{10}100^{99} \\[4pt]
&99^{100}>100^{99}
\end{align*}
(2)の考え方と解答
(2) $999^{1000}$ と $1000^{999}$ の大小を比較せよ。

さすがに(1)と同じようにはうまく行きませんよね・・・

ヒロ
同じ方法で上手く解けるなら苦労はしないよね。

ヒロ
まずは関数を設定して,その関数の増減を調べることで解いていこう。

何を $x$ と置くかを考えないといけないですね。

ヒロ
「複数回現れる数を文字で置く」のが基本だね。

じゃあ $999=x$ でも良いですか?

ヒロ
それでやってみよう。
【関数を設定する】
$999=x$ とおくと,$x^{x+1}$ と $(x+1)^x$ を比較することになる。
比較しやすいように対数をとり,$(x+1)\log x$ と $x\log(x+1)$ を比較する。
2つの差の関数 $f(x)=(x+1)\log x-x\log(x+1)$ の増減を調べよう。

ヒロ
それでは解答を書いていこう。
【(2)の解答】
$x>0$ に対し,関数 $f(x)$ を
であるから,$f'(x)>0$ となり,$f(x)$ は単調に増加する。
これと
$x>0$ に対し,関数 $f(x)$ を
\begin{align*}
f(x)=(x+1)\log x-x\log(x+1)
\end{align*}
とおくと,f(x)=(x+1)\log x-x\log(x+1)
\end{align*}
\begin{align*}
f'(x)&=\log x+\dfrac{x+1}{x}-\log(x+1)-\dfrac{x}{x+1} \\[4pt]&=\log x+1+\dfrac1x-\log(x+1)-1+\dfrac{1}{x+1} \\[4pt]&=\log x-\log(x+1)+\dfrac1x+\dfrac{1}{x+1} \\[4pt]f^{\prime\prime}(x)&=\dfrac1x-\dfrac{1}{x+1}-\dfrac{1}{x^2}-\dfrac{1}{(x+1)^2} \\[4pt]&=\dfrac{1}{x(x+1)}-\dfrac1{x^2}-\dfrac{1}{(x+1)^2} \\[4pt]&=-\dfrac{1}{x^2(x+1)}-\dfrac{1}{(x+1)^2}
\end{align*}
$f^{\prime\prime}(x)<0$ となるから,$f'(x)$ は $x>0$ において単調に減少する。f'(x)&=\log x+\dfrac{x+1}{x}-\log(x+1)-\dfrac{x}{x+1} \\[4pt]&=\log x+1+\dfrac1x-\log(x+1)-1+\dfrac{1}{x+1} \\[4pt]&=\log x-\log(x+1)+\dfrac1x+\dfrac{1}{x+1} \\[4pt]f^{\prime\prime}(x)&=\dfrac1x-\dfrac{1}{x+1}-\dfrac{1}{x^2}-\dfrac{1}{(x+1)^2} \\[4pt]&=\dfrac{1}{x(x+1)}-\dfrac1{x^2}-\dfrac{1}{(x+1)^2} \\[4pt]&=-\dfrac{1}{x^2(x+1)}-\dfrac{1}{(x+1)^2}
\end{align*}
\begin{align*}
\dlim{x\to\infty}f'(x)
&=\dlim{x\to\infty}\left(\log\dfrac{x}{x+1}+\dfrac1x+
\dfrac{1}{x+1}\right) \\[4pt]&=\dlim{x\to\infty}\left(\log\dfrac{1}{1+\dfrac1x}+
\dfrac1x+\dfrac{1}{x+1}\right)=0
\end{align*}
\dlim{x\to\infty}f'(x)
&=\dlim{x\to\infty}\left(\log\dfrac{x}{x+1}+\dfrac1x+
\dfrac{1}{x+1}\right) \\[4pt]&=\dlim{x\to\infty}\left(\log\dfrac{1}{1+\dfrac1x}+
\dfrac1x+\dfrac{1}{x+1}\right)=0
\end{align*}
であるから,$f'(x)>0$ となり,$f(x)$ は単調に増加する。
これと
\begin{align*}
f(3)&=\log3^4-\log4^3 \\[4pt]&=\log\dfrac{81}{64}>0
\end{align*}
であることからf(3)&=\log3^4-\log4^3 \\[4pt]&=\log\dfrac{81}{64}>0
\end{align*}
\begin{align*}
&f(999)>f(3)>0 \\[4pt]&\log999^{1000}-\log1000^{999}>0
\end{align*}
よって,$999^{1000}>1000^{999}$&f(999)>f(3)>0 \\[4pt]&\log999^{1000}-\log1000^{999}>0
\end{align*}
(2)の別の考え方と解答
(2) $999^{1000}$ と $1000^{999}$ の大小を比較せよ。

ヒロ
さっきは1つの文字で2つの数を表したけど,2つの文字で考える人もいるだろう。
【2つの文字を利用する場合】
$999=x,~1000=y$ とおくと,$x^y$ と $y^x$ を比較することになる。
それぞれ $\dfrac{1}{xy}$ 乗して,$x^{\frac1x}$ と $y^{\frac1y}$ を比較してもよい。
これは関数 $f(x)=x^{\frac1x}$ の増減を調べればよい。微分するためには対数微分法を使うことになるため,はじめから対数をとった関数 $g(x)=\dfrac{\log x}{x}$ の増減を調べるのがよいと分かる。

ヒロ
この考え方で解答を書くと次のようになる。
【(2)の別解】
$f(x)=\dfrac{\log x}{x}$ とおくと,
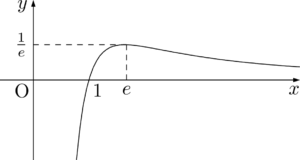
$x>e$ のとき,$f(x)$ は単調に減少するから,
$f(x)=\dfrac{\log x}{x}$ とおくと,
\begin{align*}
f'(x)=\dfrac{1-\log x}{x^2}
\end{align*}
よって,$f(x)$ の増減は次のようになる。f'(x)=\dfrac{1-\log x}{x^2}
\end{align*}
\begin{align*}
\begin{array}{|c||c|c|c|c|c|}\hline
x & 0 & \cdots & e & \cdots & \infty \\[4pt]\hline
f'(x) & & + & 0 & – & \\[4pt]\hline
f(x) & & \nearrow & \dfrac1e & \searrow & 0 \\[4pt]\hline
\end{array}
\end{align*}
したがって,グラフは下図のようになる。\begin{array}{|c||c|c|c|c|c|}\hline
x & 0 & \cdots & e & \cdots & \infty \\[4pt]\hline
f'(x) & & + & 0 & – & \\[4pt]\hline
f(x) & & \nearrow & \dfrac1e & \searrow & 0 \\[4pt]\hline
\end{array}
\end{align*}

$x>e$ のとき,$f(x)$ は単調に減少するから,
\begin{align*}
&f(999)>f(1000) \\[4pt]
&\dfrac{\log999}{999}>\dfrac{\log1000}{1000} \\[4pt]
&1000\log999>999\log1000 \\[4pt]
&\log999^{1000}>\log1000^{999} \\[4pt]
&999^{1000}>1000^{999}
\end{align*}
&f(999)>f(1000) \\[4pt]
&\dfrac{\log999}{999}>\dfrac{\log1000}{1000} \\[4pt]
&1000\log999>999\log1000 \\[4pt]
&\log999^{1000}>\log1000^{999} \\[4pt]
&999^{1000}>1000^{999}
\end{align*}
(2)の別の考え方と解答Ⅱ
(2) $999^{1000}$ と $1000^{999}$ の大小を比較せよ。

ヒロ
最後にもう1つの別解を紹介して終わろう。

ヒロ
最初に諦めた数値計算による方法でやってみよう。
【(2)の別解Ⅱ】
$\dfrac{999}{99}=10.0909\cdots$ より,
$\dfrac{999}{99}=10.0909\cdots$ より,
\begin{align*}
999&>99\times10.08 \\[4pt]&=11\Cdota3^2\Cdota\dfrac{7\Cdot9\Cdot16}{100}
\end{align*}
であるから,999&>99\times10.08 \\[4pt]&=11\Cdota3^2\Cdota\dfrac{7\Cdot9\Cdot16}{100}
\end{align*}
\begin{align*}
&\log_{10}999^{1000} \\[4pt]&>1000\log_{10}\left(11\Cdota3^2\Cdota\dfrac{7\Cdot9\Cdot16}{100}\right) \\[4pt]&=1000\log_{10}\dfrac{2^4\Cdot3^4\Cdot7\Cdot11}{100} \\[4pt]&=1000(4\log_{10}2+4\log_{10}3+\log_{10}7+\log_{10}11-2) \\[4pt]&=1000(4\times0.3010+4\times0.4771+0.8451+1.0414-2) \\[4pt]&=2998.9
\end{align*}
また&\log_{10}999^{1000} \\[4pt]&>1000\log_{10}\left(11\Cdota3^2\Cdota\dfrac{7\Cdot9\Cdot16}{100}\right) \\[4pt]&=1000\log_{10}\dfrac{2^4\Cdot3^4\Cdot7\Cdot11}{100} \\[4pt]&=1000(4\log_{10}2+4\log_{10}3+\log_{10}7+\log_{10}11-2) \\[4pt]&=1000(4\times0.3010+4\times0.4771+0.8451+1.0414-2) \\[4pt]&=2998.9
\end{align*}
\begin{align*}
\log_{10}1000^{999}&=999\times3 \\[4pt]&=2997<2998.9 \end{align*}
より, \log_{10}1000^{999}&=999\times3 \\[4pt]&=2997<2998.9 \end{align*}
\begin{align*} &\log_{10}999^{1000}>\log_{10}1000^{999} \\[4pt]&999^{1000}>1000^{999}
\end{align*}
\end{align*}

こんなの無理ですよ・・・




















