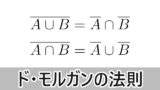【数学IA】集合の要素の個数

ある集合を考えるとき，その集合に含まれる要素の個数が無限に存在するものと個数に制限があるものに分かれます。

有限集合と無限集合要素の個数が無限に存在する集合を無限集合といい，有限個の要素からなる集合を有限集合という。

有限集合については，その集合の要素の個数を扱うことができます。

集合の要素の個数集合 $A$ の要素の個数を $n(A)$ で表す。空集合 $\emptyset$ は要素を1つももたないから，$n(\emptyset)=0$ である。

空集合と分かる形で書かれていたら，要素の個数が0であることは誰でも分かるが，$A\cap B=\emptyset$ のような「実は空集合だった」という場合だと分かりにくいので注意しよう。

【集合の要素の個数の例】
1桁の奇数全体の集合を $A$ とすると，

\begin{align*}
A=\{1,~3,~5,~7,~9\}
\end{align*}

であるから，$n(A)=5$ である。

Contents

1 和集合の要素の個数
2 集合の要素の個数に関する問題
3 集合の要素の個数に関する問題2

和集合の要素の個数

ヒロ

集合の要素の個数についても，ド・モルガンの法則が重要になってくる。

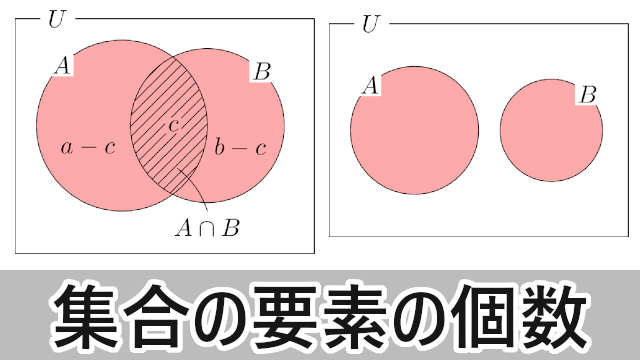
和集合の要素の個数全体集合 $U$ の2つの部分集合 $A,~B$ の要素の個数について次の式が成り立つ。

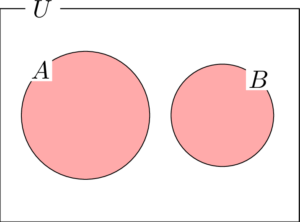
\begin{align*}
&n(A\cap B)=n(A)+n(B)-n(A\cap B)
\end{align*}

$A\cap B=\emptyset$ のときは

\begin{align*}
n(A\cup B)=n(A)+n(B)
\end{align*}

ここで

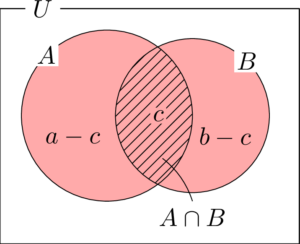
\begin{align*}
n(A)=a,~n(B)=b,~n(A\cap B)=c
\end{align*}

とすると

\begin{align*}
n(A\cap\overline{B})&=n(A)-n(A\cap B) \\[4pt]&=a-c \\[4pt]n(\overline{A}\cap B)&=n(B)-n(A\cap B) \\[4pt]&=b-c
\end{align*}

となるから，次の図のようになる。

このとき

\begin{align*}
n(A\cup B)&=(a-c)+c+(b-c) \\[4pt]&=a+b-c \\[4pt]&=n(A)+n(B)-n(A\cap B)
\end{align*}

となる。特に $A\cap B=\emptyset$ のときは $n(A\cap B)=0$ であるから

\begin{align*}
n(A\cup B)=n(A)+n(B)
\end{align*}

集合の要素の個数に関する問題

ヒロ

それでは実際に定期テストで出題された問題を解いてみよう。

問題$U$ を全体集合とし，$n(U)=50$ とする。$U$ の部分集合 $A,~B$ について，

\begin{align*}
n(\overline{A}\cap B)=18,~n(A\cap B)=8,~n(\overline{A}\cap\overline{B})=10
\end{align*}

であるとき，次の値を求めよ。
(1) $n(A\cup B)$
(2) $n(B)$
(3) $n(A\cup\overline{B})$
(4) $n(\overline{A}\cup\overline{B})$

ヒロ

ベン図を描いて考えよう。

【ベン図を描く】
$n(A\cap B)\neq0$ だから，$A\cap B$ が存在することが分かる次のような図を描く。

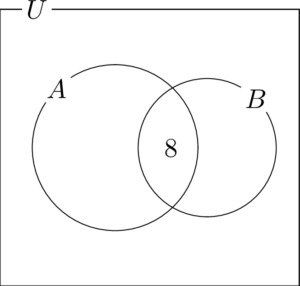
$n(A\cap B)=8$ だから $A$ と $B$ の共通部分に8を書く。

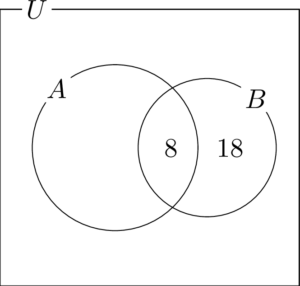
$n(\overline{A}\cap B)=18$ だから，$A$ の外側で $B$ の内側の部分に18を書く。

$n(\overline{A}\cap\overline{B})=10$ だから，$A$ と $B$ の両方の外側の部分に10を書く。

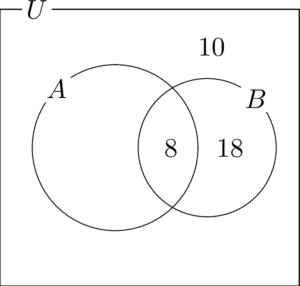
$n(U)=50$ だから，残った部分，つまり $A$ の内側で $B$ の外側の部分が14であることが分かる。

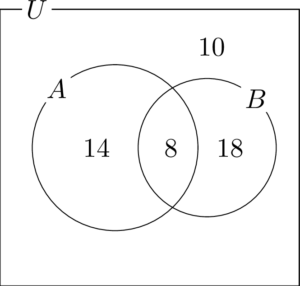
ヒロ

ベン図が完成したので問題に答えていこう。

ヒロ

それぞれの式が表す部分を正確に把握することができれば簡単だろう。

【解答】
(1) $n(A\cup B)=40$
(2) $n(B)=26$
(3) $n(A\cup\overline{B})=32$
(4) $n(\overline{A}\cup\overline{B})=42$

集合の要素の個数に関する問題2

ヒロ

次の問題も定期テストで出題された問題。

問題100から200までの整数のうち，次のような整数は何個あるか。
(1) 6で割り切れる整数
(2) 6で割り切れるが8では割り切れない整数

ヒロ

倍数の個数の数え方をマスターしよう。

連続する整数の個数

\begin{align*}
(連続する自然数の個数)=(最後の数)-(最初の数)+1
\end{align*}

ヒロ

このことを丁寧に説明すると次のようになる。

【連続する整数の個数】
連続する自然数

\begin{align*}
1,~2,~3,~\cdots,~n
\end{align*}

の個数は $n$ 個である。これは説明不要だろう。
また，

\begin{align*}
a,~a+1,~a+2,~\cdots,~b-1,~b
\end{align*}

の個数は $b-a+1$ 個である。これは自然数が書かれたシールを貼っていくという考え方をすると次のようになる。
$a$ に①のシールを貼る。
$a+1$ には②のシールを貼る。このようにシールを貼っていくと，$b$ に貼られたシールが求める個数となる。
実際の数 $a$ とシールの番号との差に着目すると，$a-1$ であることが分かる。
数 $a$ とシール①の場合は，差は $a-1$
また，数 $a+1$ とシール②の場合も，差は $(a+1)-2=a-1$
数が1ずつ増加して，シールの番号も1ずつ増加しているから，差は $a-1$ で変わらないことも分かるはず。
ということは $b$ に付けられるシールは

\begin{align*}
b+(a-1)=a+b-1
\end{align*}

となる。つまり，連続する自然数の個数を求める場合は

\begin{align*}
(連続する自然数の個数)=(最後の数)-(最初の数)+1
\end{align*}

で求められることが分かる。

ヒロ

それでは問題を解いていこう。

(1) 100から200までの整数のうち，6で割り切れる整数の個数

【(1)の考え方と解答】
100から200までの整数のうち，6で割り切れる整数は

\begin{align*}
6\times17,~6\times18,~\cdots,~6\times33
\end{align*}

となるから，求める個数は

\begin{align*}
33-17+1=17~個
\end{align*}

(2) 100から200までの整数のうち，6で割り切れるが8で割り切れない整数の個数

【(2)の考え方と解答】
100から200までの整数を全体集合 $U$ とし，$U$ の要素で6で割り切れる整数を
集合 $A$，8で割り切れる整数を集合 $B$ とすると，6で割り切れるが8で割り切れない整数を表す集合は次の斜線部分となる。

ここで $A\cap B$ は6と8の最小公倍数24の倍数を表し

\begin{align*}
24\times5,~24\times6,~24\times7,~24\times8
\end{align*}

を考えると $n(A\cap B)=4$ である。
したがって，ベン図より

\begin{align*}
n(A\cap\overline{B})&=n(A)-n(A\cap B) \\[4pt]&=17-4 \\[4pt]&=13
\end{align*}

よって，求める個数は13個である。