Contents
アポロニウスの円に関する問題【藤田医科大】
2020年 藤田医科大$xy$ 平面上に点A$(3,~0)$,B$(0,~4)$ がある。$\text{PA}:\text{PB}=3:2$ となる点Pの軌跡を表す図形の周の長さは $\myhako\,\pi$ である。
【考え方と解答】
$\text{PA}:\text{PB}=3:2$ より
$\text{PA}:\text{PB}=3:2$ より
\begin{align*}
&2\text{PA}=3\text{PB} \\[4pt]
&4\text{PA}^2=9\text{PB}^2
\end{align*}
点Pの座標を $(X,~Y)$ とすると,&2\text{PA}=3\text{PB} \\[4pt]
&4\text{PA}^2=9\text{PB}^2
\end{align*}
\begin{align*}
&4\{(X-3)^2+Y^2\}=9\{X^2+(Y-4)^2\} \\[4pt]
&5X^2+24X+5Y^2-72Y=-108 \\[4pt]
&\left(X+\dfrac{12}{5}\right)^2+\left(Y-\dfrac{36}{5}\right)^2=36
\end{align*}
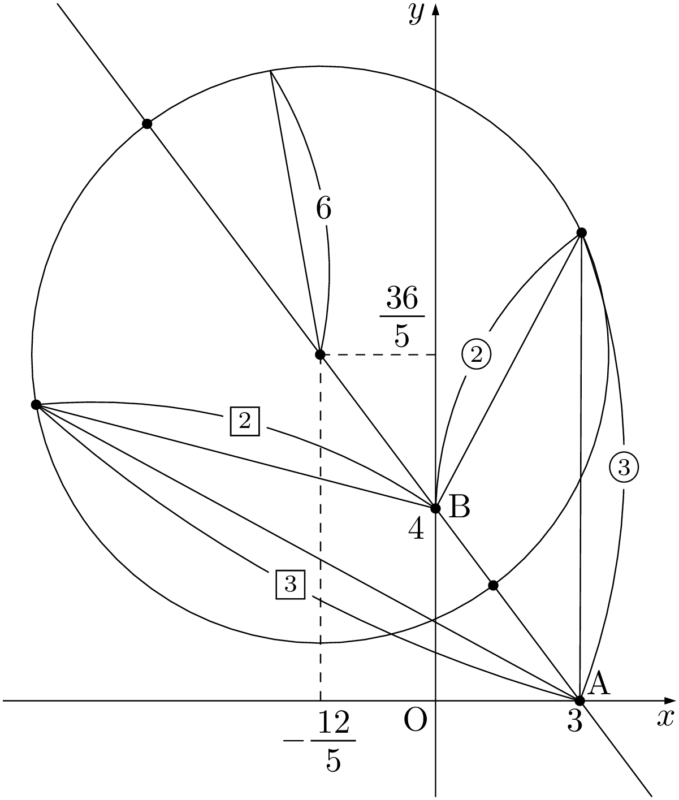
よって,点Pの軌跡は,中心 $\left(-\dfrac{12}{5},~\dfrac{36}{5}\right)$,半径6の円であるから,その周の長さは&4\{(X-3)^2+Y^2\}=9\{X^2+(Y-4)^2\} \\[4pt]
&5X^2+24X+5Y^2-72Y=-108 \\[4pt]
&\left(X+\dfrac{12}{5}\right)^2+\left(Y-\dfrac{36}{5}\right)^2=36
\end{align*}
\begin{align*}
2\pi\times6=12\pi
\end{align*}
2\pi\times6=12\pi
\end{align*}


ヒロ
アポロニウスの円に関する知識があると,次のように空欄を埋めることができる。
【別の考え方と解答】
点Pの軌跡は線分ABを $3:2$ に内分する点Qと外分する点Rを直径の両端とする円である。A$(3,~0)$,B$(0,~4)$ より
点Pの軌跡は線分ABを $3:2$ に内分する点Qと外分する点Rを直径の両端とする円である。A$(3,~0)$,B$(0,~4)$ より
\begin{align*}
\text{Q}\left(\dfrac{6}{5},~\dfrac{12}{5}\right),~\text{R}(-6,~12)
\end{align*}
となる。よって\text{Q}\left(\dfrac{6}{5},~\dfrac{12}{5}\right),~\text{R}(-6,~12)
\end{align*}
\begin{align*}
\text{QR}&=\sqrt{\left(\dfrac{6}{5}+6\right)^2+\left(\dfrac{12}{5}-12\right)^2} \\[4pt]
&=\sqrt{\dfrac{36^2}{5^2}+\dfrac{48^2}{5^2}} \\[4pt]
&=\dfrac{12}{5}\sqrt{9+16}=12
\end{align*}
したがって,求める長さは\text{QR}&=\sqrt{\left(\dfrac{6}{5}+6\right)^2+\left(\dfrac{12}{5}-12\right)^2} \\[4pt]
&=\sqrt{\dfrac{36^2}{5^2}+\dfrac{48^2}{5^2}} \\[4pt]
&=\dfrac{12}{5}\sqrt{9+16}=12
\end{align*}
\begin{align*}
\pi\times\text{QR}=12\pi
\end{align*}
\pi\times\text{QR}=12\pi
\end{align*}

ヒロ
空欄を埋めるだけなら座標を求める必要はない。
【座標を求めない考え方と解答】
線分ABを $3:2$ に内分する点Qと外分する点Rを図示すると,次のようになる。
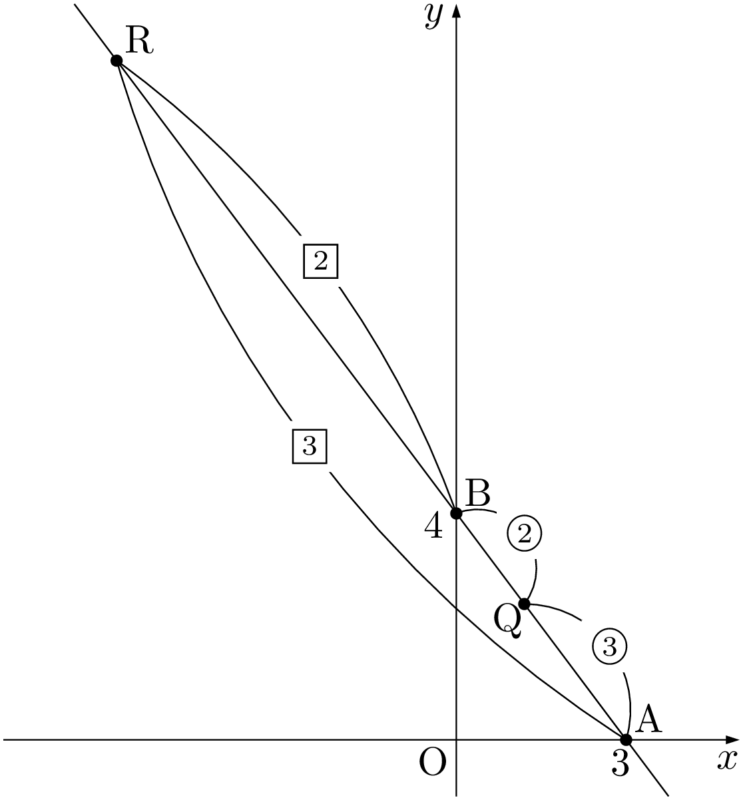
真面目に図を描けば上図のようになるが,QRの長さが分かれば良いので,実際には,次のように数直線上に4点A,B,Q,Rをとって考えれば良い。

ABの長さに着目すると,$\fbox{1}=⑤$ であることが分かるから,$\text{BR}=2\text{AB}$ となる。また,$\text{QB}=\dfrac{2}{5}\text{AB}$ であることから
したがって
線分ABを $3:2$ に内分する点Qと外分する点Rを図示すると,次のようになる。

真面目に図を描けば上図のようになるが,QRの長さが分かれば良いので,実際には,次のように数直線上に4点A,B,Q,Rをとって考えれば良い。

ABの長さに着目すると,$\fbox{1}=⑤$ であることが分かるから,$\text{BR}=2\text{AB}$ となる。また,$\text{QB}=\dfrac{2}{5}\text{AB}$ であることから
\begin{align*}
\text{QR}&=\text{QB}+\text{BR} \\[4pt]
&=\dfrac{2}{5}\text{AB}+2\text{AB} \\[4pt]
&=\dfrac{12}{5}\text{AB}
\end{align*}
$\sankaku{OAB}$ は $3:4:5$ の有名直角三角形であることが分かるから,$\text{AB}=5$ である。\text{QR}&=\text{QB}+\text{BR} \\[4pt]
&=\dfrac{2}{5}\text{AB}+2\text{AB} \\[4pt]
&=\dfrac{12}{5}\text{AB}
\end{align*}
したがって
\begin{align*}
\text{QR}=\dfrac{12}{5}\times5=12
\end{align*}
となるから,求める点Pの軌跡の長さは\text{QR}=\dfrac{12}{5}\times5=12
\end{align*}
\begin{align*}
\pi\times\text{QR}=12\pi
\end{align*}
\pi\times\text{QR}=12\pi
\end{align*}