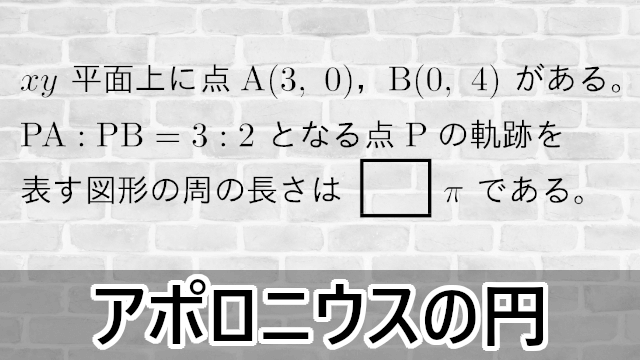
Contents
アポロニウスの円に関する問題【常葉大】
2018年 常葉大点A$(-1,~-4)$,B$(2,~2)$ とする。線分ABを $2:1$ に内分する点の座標は $\left(\myhako,~\myhako\right)$
線分ABを $2:1$ に外分する点の座標は $\left(\myhako,~\myhako\right)$ である。
$\text{AP}:\text{BP}=2:1$ を満たす点Pの軌跡の方程式は
線分ABを $2:1$ に外分する点の座標は $\left(\myhako,~\myhako\right)$ である。
$\text{AP}:\text{BP}=2:1$ を満たす点Pの軌跡の方程式は
\begin{align*}
x^2+y^2-\myhako\,x-\myhako\,y+\myhako=0
\end{align*}
である。x^2+y^2-\myhako\,x-\myhako\,y+\myhako=0
\end{align*}
【考え方と解答】
一見,ただ内分点と外分点を求めるだけかと思ったら,軌跡の問題がある。見た瞬間にアポロニウスの円に関する問題だと分かり,それが分かる人にとっては,内分点と外分点が直径の両端になることも分かる問題である。
まずは内分点の座標から求めよう。
次に外分点の座標を求める。
点Pの軌跡は上で求めた内分点と外分点を直径の両端とする円であることを知っているから,サクッと求めてしまおう。
一見,ただ内分点と外分点を求めるだけかと思ったら,軌跡の問題がある。見た瞬間にアポロニウスの円に関する問題だと分かり,それが分かる人にとっては,内分点と外分点が直径の両端になることも分かる問題である。
まずは内分点の座標から求めよう。
\begin{align*}
&x=\dfrac{2\Cdot2+1\Cdot(-1)}{2+1}=1 \\[4pt]
&y=\dfrac{2\Cdot2+1\Cdot(-4)}{2+1}=0
\end{align*}
よって,内分点は $(1,~0)$&x=\dfrac{2\Cdot2+1\Cdot(-1)}{2+1}=1 \\[4pt]
&y=\dfrac{2\Cdot2+1\Cdot(-4)}{2+1}=0
\end{align*}
次に外分点の座標を求める。
\begin{align*}
&x=\dfrac{2\Cdot2-1\Cdot(-1)}{2-1}=5 \\[4pt]
&y=\dfrac{2\Cdot2-1\Cdot(-4)}{2-1}=8
\end{align*}
よって,外分点は $(5,~8)$&x=\dfrac{2\Cdot2-1\Cdot(-1)}{2-1}=5 \\[4pt]
&y=\dfrac{2\Cdot2-1\Cdot(-4)}{2-1}=8
\end{align*}
点Pの軌跡は上で求めた内分点と外分点を直径の両端とする円であることを知っているから,サクッと求めてしまおう。
\begin{align*}
&(x-1)(x-5)+y(y-8)=0 \\[4pt]
&x^2+y^2-6x-8y+5=0
\end{align*}
&(x-1)(x-5)+y(y-8)=0 \\[4pt]
&x^2+y^2-6x-8y+5=0
\end{align*}